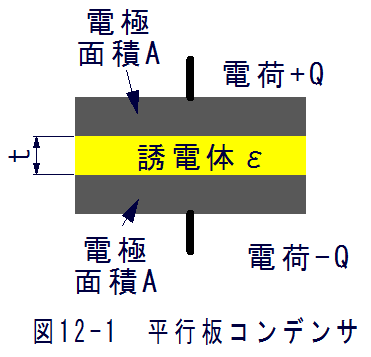
平行板コンデンサ図12-1に示すように、電荷を蓄える目的で２つの電極を絶縁物を隔てておいたものをコンデンサと いいます。この絶縁体を誘電体といいます。
コンデンサの両極間にV(V)の電圧を与えたとき、一方の極の電荷が+Q(C)であるとすれば、他方の 極板には必ず-Q(C)の電荷が拘束されます。そこで
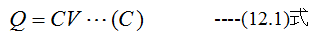
(12.1)式で定義された係数Cをコンデンサの静電容量といい、単位はファラッド（F)とします。実用的に はμFやpFが用いられます。
例題12-10.08μFのコンデンサに200Vを加えたときに蓄えられる電荷量はいくらか？
解答
平行板コンデンサの静電容量
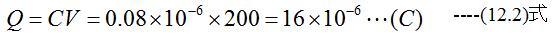
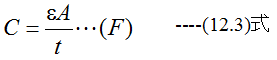
となります。
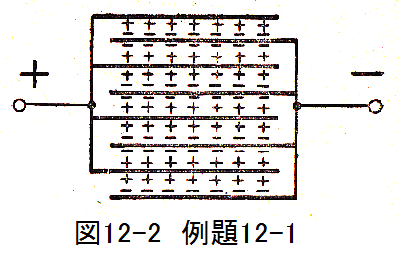
例題12-2図12-2に示すように、有効面積50cm2の金属板8枚を2mmの間隔に配置し、一つおきに同極につ なぎ比誘電率2.3の油を充たしたときの容量はいくらか？
解答
図12-2から実質の面積Aは1枚の有効面積の7倍となります。したがって
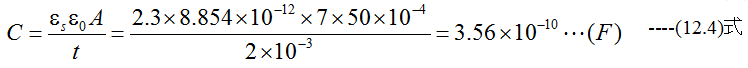
コンデンサの合成（１）直列接続
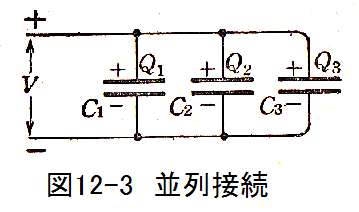
図12-3に示すようにコンデンサを並列に接続した場合、各コンデンサに同じ電圧Vがかかります。
合成容量をC0とした場合
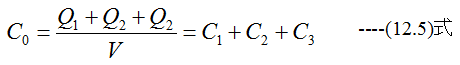
となります。
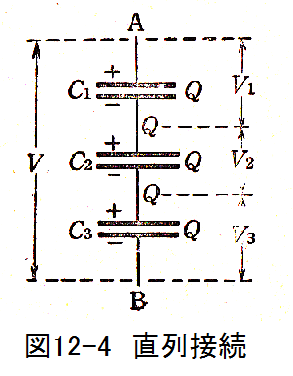
（２）並列接続図12-4に示すようにコンデンサを直列に接続した場合、各コンデンサには同じ電荷量Qが蓄積されます。
合成容量をC0とした場合
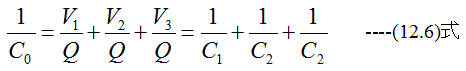
となります。
例題12-34μFと6μFと10μFの並列および直列接続の容量を求めよ。
解答
並列の場合
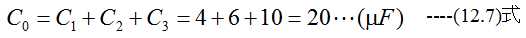
直列の場合
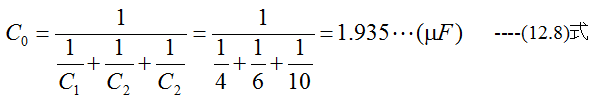
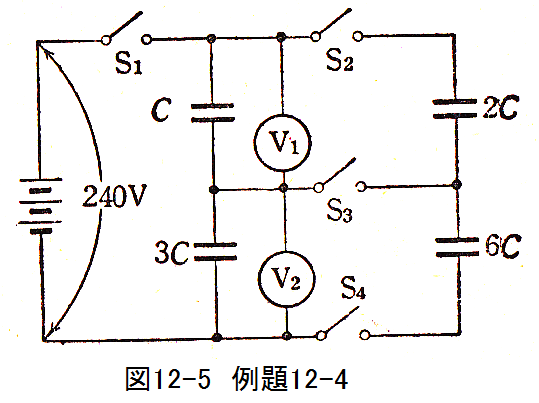
例題12-4図12-5に示す回路において、下記条件における電圧V1とV2を求めよ。
(a)スイッチS1だけ閉じた時
(b)次にS1を開き、S2とS3を閉じた時
(c)さらにS4を閉じた時
(d)さらにS3を開いた時
解答
(a)スイッチS1だけ閉じた時合成容量は
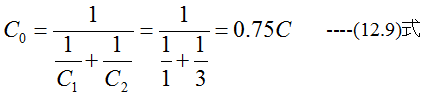
電圧V1とV2の値は
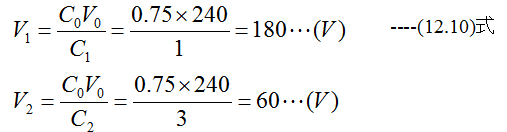
(b)次にS1を開き、S2とS3を閉じた時
Cと2Cの並列容量Cbは
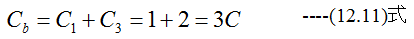
電圧V1は
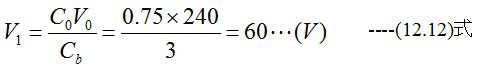
電圧V2は
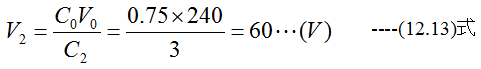
(c)さらにS4を閉じた時
3Cと6Cの並列容量Ccは
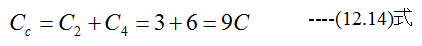
電圧V1は
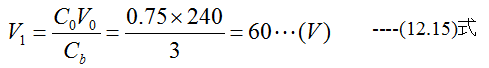
電圧V2は
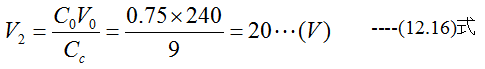
(d)さらにS3を開いた時は電流が流れないため、V1とV2は変化しません。
コンデンサに蓄えられるエネルギーC(F)のコンデンサに加える電圧V(V)をt(s)かかって均等にに上昇した場合平均電流Iave（A)は
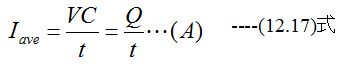
です。そして、その平均電圧はV/2です。したがってコンデンサの充電に要したエネルギーWは
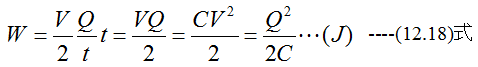
の関係が成立します。(12.16)式は時間ｔと無関係に成立します。すなわち、電圧Vにおける微 小電荷dQによるエネルギーdWは
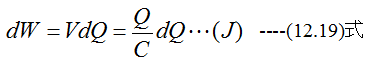
です。電荷量が0〜Qまでの積分は
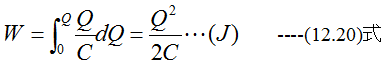
となり、時間とは無関係に成立します。
例題12-5あるコンデンサに加える電圧を500Vから8500Vまで2ｓ間流したら平均電流が0.5mAであった。コンデンサの容量はいくらか？
解答
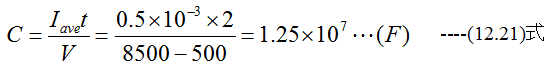
例題12-60.2μFのコンデンサに1000Vを加えたときのエネルギーはいくらか？
解答
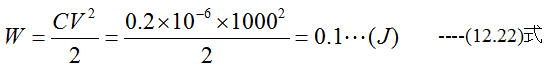
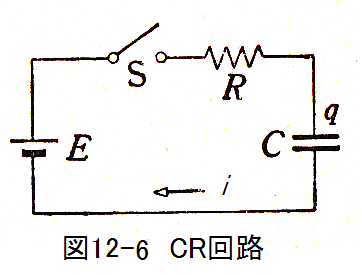
CR回路特性図12-6に示すCR回路において、t=0における電荷qはゼロとします。スイッチSを閉じ てからt時間後の電流Iはどうなるでしょう？
オームの法則から
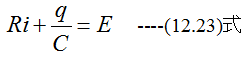
また
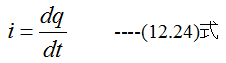
(12.23)式に(12.24)式を代入して整理すると
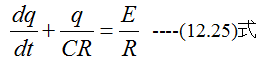
(12.25)式は1階線形微分方程式です。1階線形微分方程式の一般形は
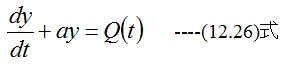
であり、一般解は
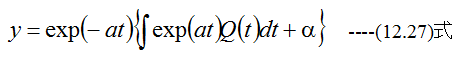
となります。したがって
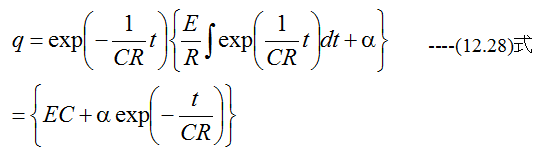
となります。t=0でq=0の条件を代入すると
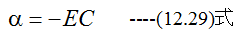
したがって
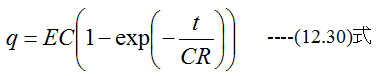
(12.30)式を微分すると
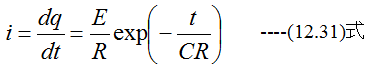
となります。
例題12-70.5μFのコンデンサに2000Ωの抵抗を通じて1000Vを加えたときの電流を0.1ms刻みで2msまで計算してグラフにせよ。
解答
解答のＥＸＣＥＬ計算表は下記で参照できます。
「12-1.xls 」にいく。 ．インダクタンスに蓄えられるエネルギー自己インダクタンスがL(H)のコイルに電流をゼロからI（A)までt(s)かかって均等にに上昇した 場合平均電圧Eave（V)は
です。したがってインダクタンスに蓄えられるエネルギーWは
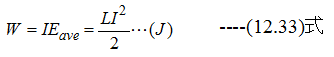
の関係が成立します。(12.31)式は時間ｔと無関係に成立します。すなわち、微小電流変化dIに よるエネルギーdWは
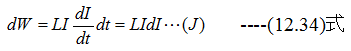
です。電流が0〜Iまでの積分は
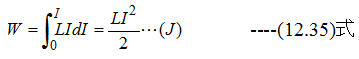
となり、時間とは無関係に成立します。
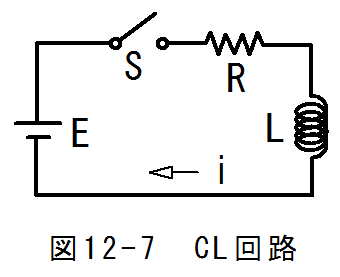
CL回路特性図12-7に示すCL回路において、t=0における電流iはゼロとします。スイッチSを閉じてからt時間後の電流 iはどうなるでしょう？
オームの法則から
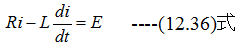
従って
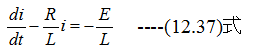
(12.37)式は1階線形微分方程式です。1階線形微分方程式の一般形は
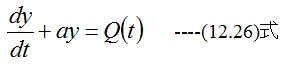
であり、一般解は
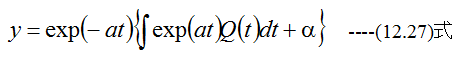
となります。したがって
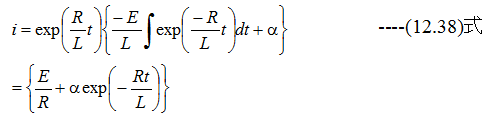
となります。t=0でi=0の条件を代入すると
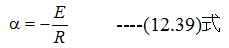
したがって
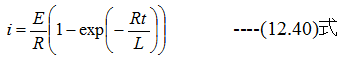
となります。
例題12-81mHのインダクタンスに1Ωの抵抗を通じて100Vを加えたときの電流を0.2ms刻みで5msまで計算してグラフにせよ。
解答
解答のＥＸＣＥＬ計算表は下記で参照できます。
「12-2.xls 」にいく。