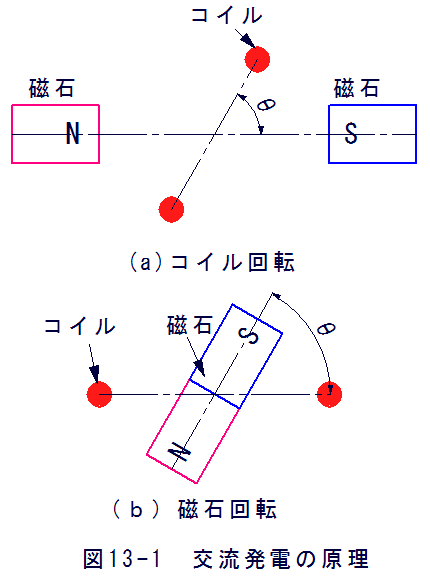
交流発電の原理図13-1に交流発電の原理を示します。(a)コイル回転と(b)磁石回転がありますが磁界とコイルの相対運動は同じとなります。
磁束密度B〔T〕（〔Wb/m2〕）、コイルの胴体の長さl〔m〕、導体の移動方向が磁界と直角で速度がv〔m/s〕とすると、導体が1s 間に移動する距離vtはv×1=v〔m〕、導体が磁束と交差する面積はlvsinθ〔m2〕、よって、1s 間の磁束の変化数は-Blvcosθ、よって起電力Eは
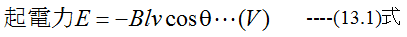
回転子の速度v〔m／s〕は直径D〔m〕、1秒間の回転数をn回〔rps〕とすると
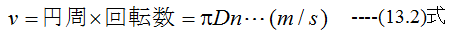
磁束密度（平均）B〔T〕は1極当たりの磁束をΦ〔Wb〕、極数をp、導体の長さをl〔m〕とすると、
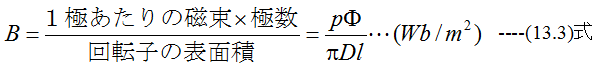
(13.1)式に(13.2)式と(13.2)式を代入すると
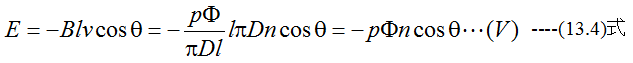
と比較的簡単な式となります。(13.4)式はコイル１個当たりの起電力となりますが、全コイルの 巻き数Zとコイルの並列結線数aで起電力は変化します。起電力の倍率mは
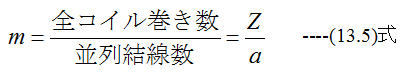
(13.4)式と(13.5)式から一般てきな交流発電機の起電力は
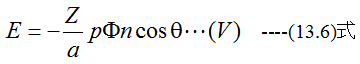
となります。(13.6)式は正弦波を表わしており、角速度をω、最大値をEmとし、位相を変化させれば
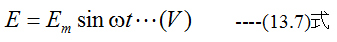
と表わすことができます。全くおなじ2点間を「１サイクル」といい、１サイクルの要する時間を「周期」といいます。
実効値交流の瞬時値はたえず変化します。それで、R(Ω）の抵抗に電流が流れた場合の発熱において、直流 と等しい値で実効値を定義します。すなわち
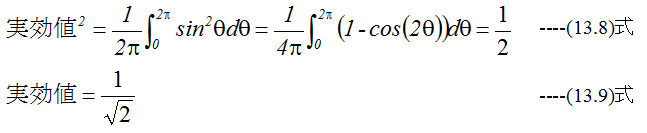
となります。 またθが0からπの平均値は
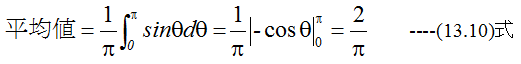
となります。 また、一般的に
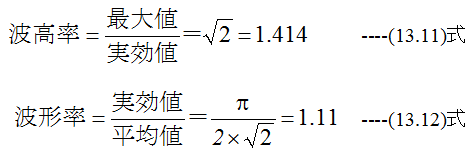
といいます。
例題13-1200Vの交流電圧と最大値と平均値はいくらか？
解答
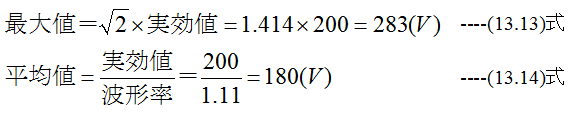
リアクタンス電圧いま、L(H)の純インダクタンス（抵抗が無視できるもの）に
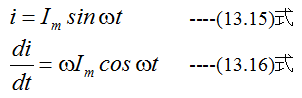
の電流を流した場合、その端子電圧は
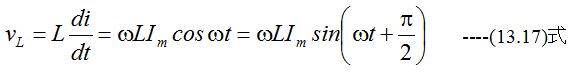
となります。すなわち最大値がωLImで電流よりも位相がπ/2進んだ電圧となります。 逆に
の電圧を加えた場合
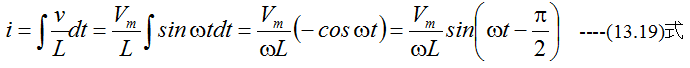
となります。すなわち、最大値がVm/ωLで位相がπ/2遅れた電流が流れることになります。つまり、L(H)のインダクタンスはωL[Ω]の抵抗と同様の電流阻止作用があるおとになります。
それで、これをリアクタンス（Xで表わす）と名づけて抵抗と同様に扱い、オーム[Ω]を単位とします。
例題13-210mHのインダクタンスに50Hz、100Vの電圧を加えたら何A流れるか？
解答
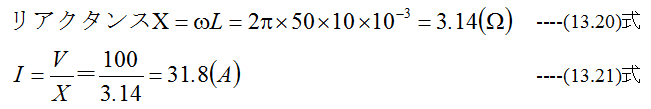
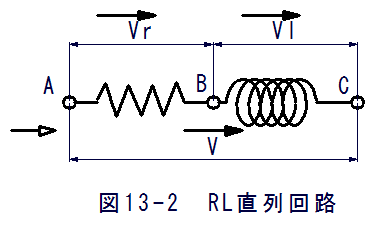
RL直列回路図13-2に示すようにRとLが直列の回路において
の電流が流れたとすると
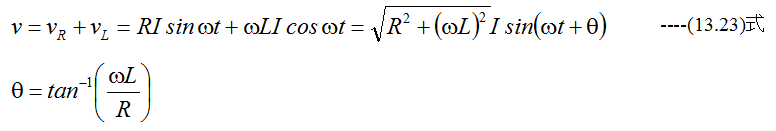
となります。 そこで、逆にV(V)をこの直列回路に加えると
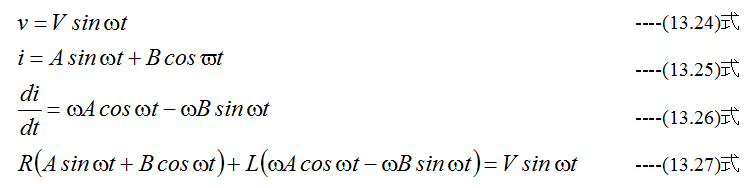
したがって
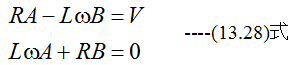
連立方程式を解くと
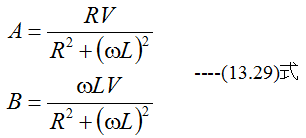
したがって電流は
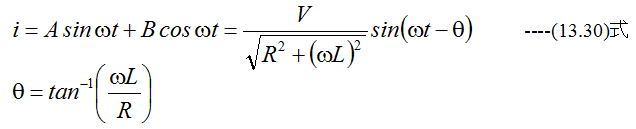
となります。そこで
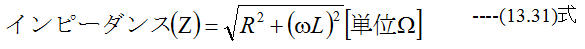
とするならば、抵抗Rと同一の電流阻止作用をすることになります。
例題13-3抵抗8Ω、リアクタンス6Ωのコイルに200Vの正弦波交流電圧を加えると何A流れる か？またこのコイルのインピーダンスはいくらか？
解答
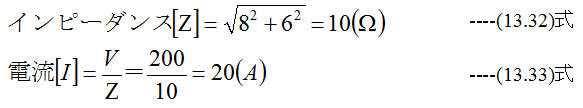
RLC直列回路C(F)コンデンサに
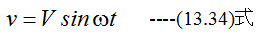
の電圧を加えるとコンデンサに蓄えられる電荷は
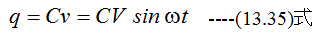
です。電流は
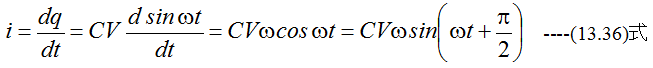
となります。抵抗Rと同等な容量リアクタンスは
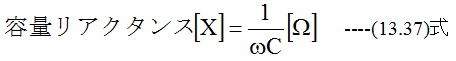
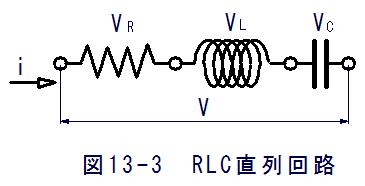
となります。 図13-3に示すRLC直列回路の両端に
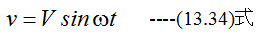
を加えると
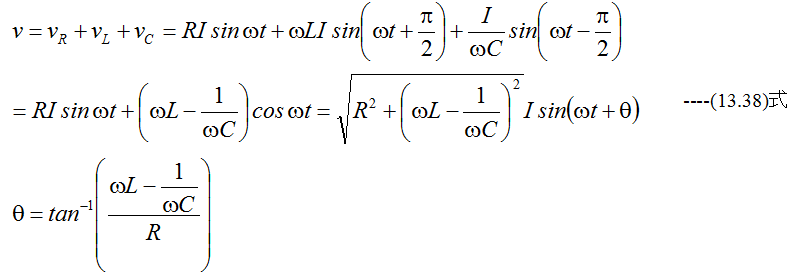
となります。従ってインピーダンス（Z)は
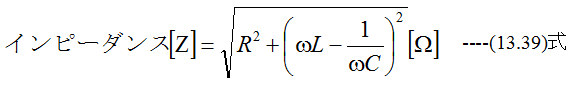
となります。インピーダンス（Z)は通常抵抗Rと同様に扱うことができま す。θがプラスのとき、電流は電圧より位相がθ遅れます。
１４章：ベクトル表示と記号法に行く。