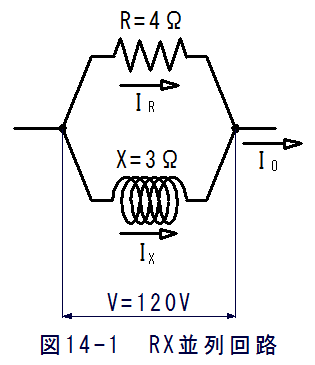
ベクトル表示図14-1に示す抵抗R=4Ωと誘導リアクタンスX=3Ωの並列回路に120Vの交流電圧を加えた場合 の合成電流が何Aか？これを例にとって考えます。
これまでの知識では
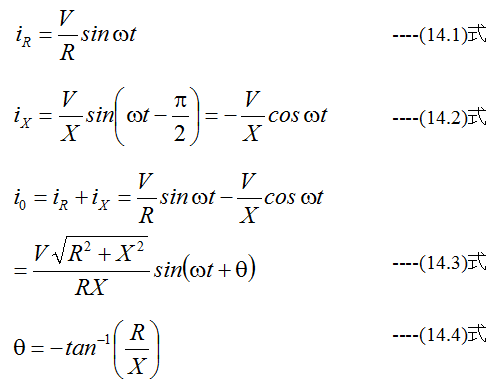
となり、(14.3)式と(14.4)式から
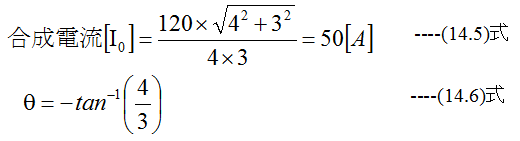
となりますが、結構めんどうです。(14.5)式と(14.6)式は大きさと方向を持つ量であり、こ れをベクトルに置き換えることができます。
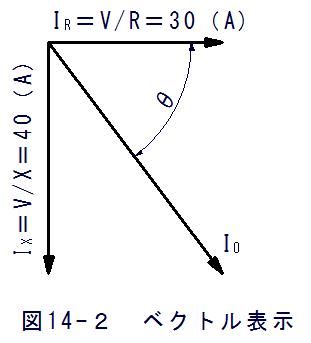(14.1)式と(14.2)式の結果をベクトルで表示すれば図14-2に示すようになります。大きさと方向を持つ量はベクトルで表示することにより、その大きさと方向を直感的な理解を容易とします。
記号法数学的にみれば、ベクトルと複素式は異なります。正弦波交流はベクトルであるから電圧や電流も複素式で表わすことができる。
そして位相がπ/2進むのは「j」をかけると約束し、π/2遅れるのは「-j」をかけると約束します。そして「j」を虚数部とする複素数として扱う手法を「記号法」といいます。
一般電気では、紙面の節約のため計算方法のみの解説になっています。
大変便利な計算手法なのですが、電気の計算になれない者のとっては、すなおに鵜呑みにしてよいか？疑問が生じると思います。
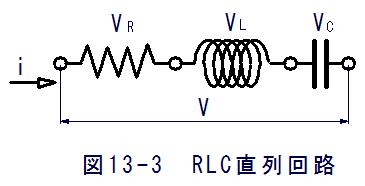図13-3のRLC直列回路において基礎方程式は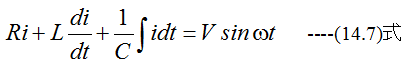
(14.7)式を満足する解は数学的には無限に存在しますが交流理論では角速度がωの正弦波のみに注目します。従 って特殊解は
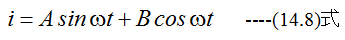
となります。(14.7)式に(14.8)式を代入して定数AとBを決定すれば解が求まることになります。定数の決定はさほど難しくはありません。しかし、しかし、扱う数は実数のみであり複素数はでてきません。
ここで、(14.7)式を複素数の式に変更します。
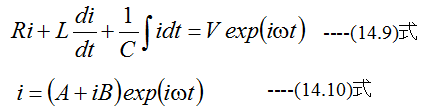
(14.9)式に(14.10)式を代入して定数AとBを決定できます。このほうが式の変形が容易となります。
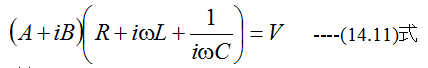
したがって
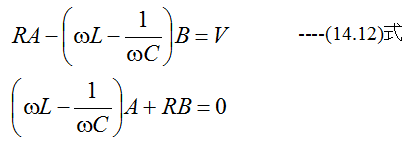
(14.12)式の解は
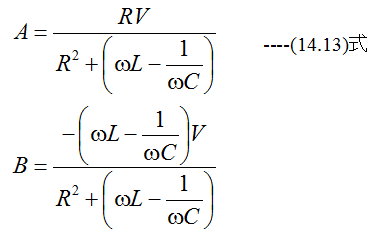
電流Iの絶対値は
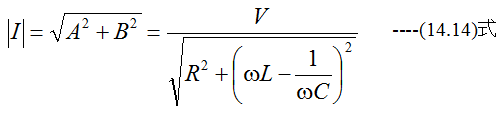
電流Iの位相は
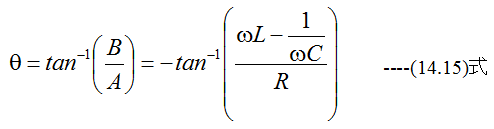
となります。一見難解にみえますが、複素数を使用したほうがスマートに式を展開できます。
一般数学において虚数の記号は「i」ですが、電気工学では「j」を使用します。これにより複素数の公式がそのまま適用できます。
位相がπ/2進むのは「j」をかけ、π/2遅れるのは「-j」をかけるのは複素数の基本公式です。
図13-3のRLC直列回路において電流Iが流れた場合の電圧Vは比較的簡単に計算できます。複素電圧は
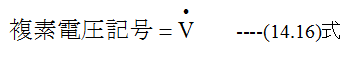
と記述します。
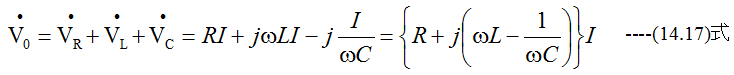
したがって、抵抗Rはそのまま、誘導リアクタンスには「j」、容量リアクタンスには「-j」をかけるこ とに約束すると、直列インピーダンスは単に加法となり、オームの法則がそのまま使えます。
すなわち
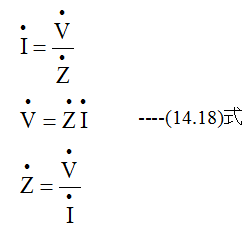
実効値がほしければ、それぞれ複素式の絶対値を求めればよい。すなわち
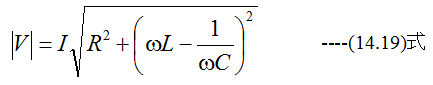
記号法使用例図14-1のRX並列回路に記号法を適用すと
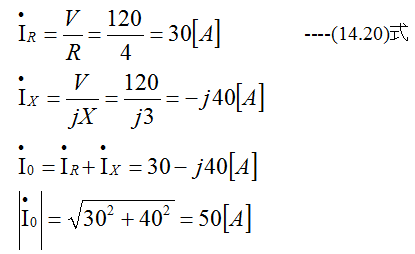
となります。
インピーダンス（Z)の結合（１）抵抗の直列結合
ｎ個の抵抗Ri(i=1,2,…,n）を直列結合した場合の合成抵抗Rは
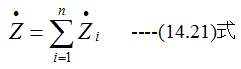
となります。
（２） 抵抗の並列結合
ｎ個の抵抗Ri(i=1,2,…,n）を並列結合した場合の合成抵抗Rは
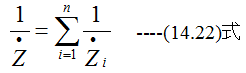
となります。
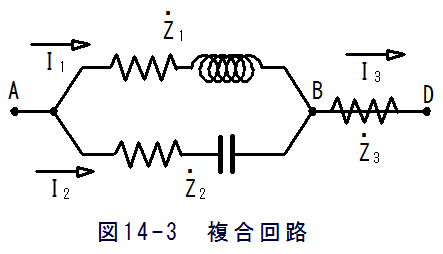（３）複合回路にインピーダンス図14-3に示す複合回路のインピーダンスは
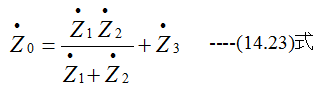
となります。
直列共振図13-3において
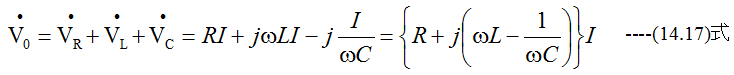
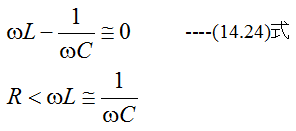
のとき共振します。このとき
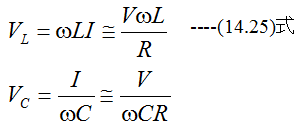
例題14-1抵抗4Ω、誘導リアクタンス1000Ω、容量リアクタンス997Ωの直列回路に100Vの正弦波交流電圧を加 えたとき、誘導リアクタンスの端子電圧はいくらか？これは供給電圧の何倍か？
解答
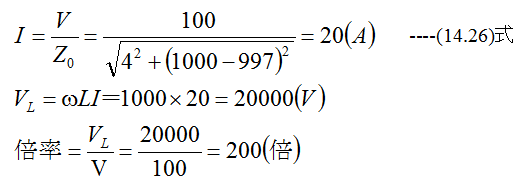
例題14-210ΩのRと10mHのLと1μFのCとが直列にあるとき、この回路が共振する周波数はいくらか？
解答
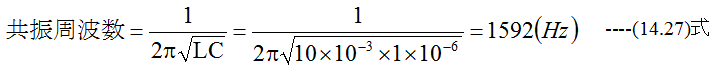
並列共振図14-3において、AB間の電圧をVとすると
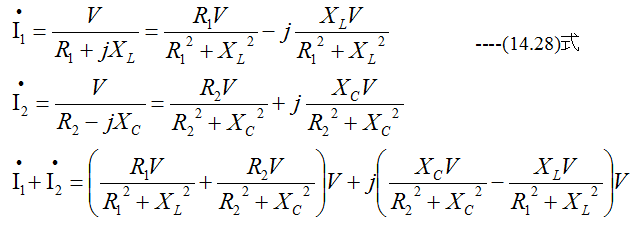
となります。ここで
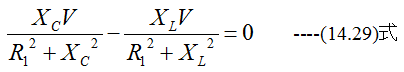
の場合、合成電流（I1+I2）は最小となるが並列回路の電流は非常に大きくなる。これを並列共振といいます。
１５章：交流電力に行く。