キルヒホッフの法則第1法則：1点に集まる代数和はゼロである。
第2法則：ある任意の回路で、ある向きに一回りしたときは、その起電力の代数和は電圧降下の代数和と等しい。
第1法則は電流はたまることができないということ。第2法則はオームの法則の拡張にすぎない。
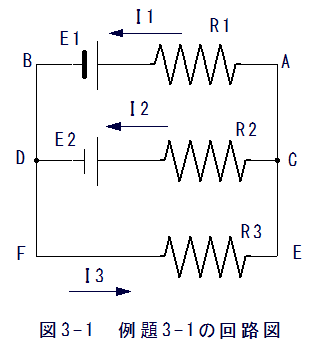
例題3-1図3-1に示す回路の電流I1とI2とI3を求めよ。
解答
まず、D点での電流を考えます。流入するのは、I1とI2です。流出するのはI3です。流入 をプラス、流出をマイナスとすれば
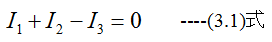
次の回路ABDCAでキルヒホッフの第2法則を適用すると
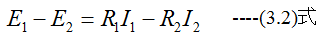
同様に回路CDFECでキルヒホッフの第2法則を適用すると
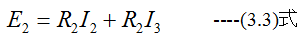
上記式は下記の３元連立１次方程式となります。
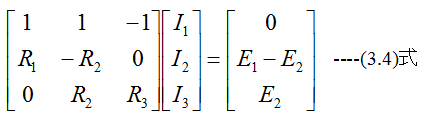
下記の計算条件において
| 記号 | 値 | 記号 | 値 |
| R1 | 15 | E1 | 20 |
| R2 | 20 | E2 | 15 |
| R3 | 10 |
| 記号 | 代数値 | VBA値 |
| I1 | 0.692307692 | 0.692307692 |
| I2 | 0.269230769 | 0.269230769 |
| I3 | 0.961538462 | 0.961538462 |
ダウンロード後はダブルクリックで解凍してから使用してください。
[例題3-1専用ソフト]をダウンロードする。
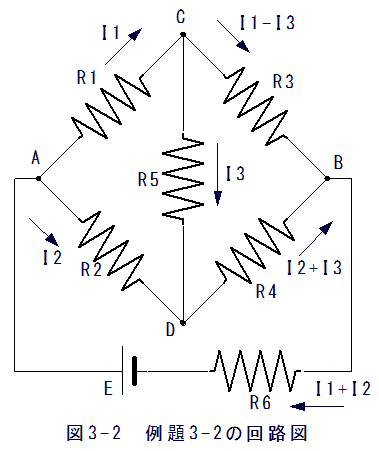
例題3-2図3-2に示すブリッジ回路の電流I1とI2とI3を求めよ。
解答
AC間をI1、AD間をI2、CD間をI3とするならば、第1法則より、CB間はI1-I3、DB間はI2+I3、BA間はI2+I3となります。
ACDAの網目では第2法則より
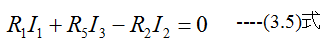
CDBCの網目では
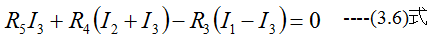
ADBAの網目では
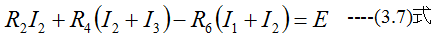
これらを整理すると
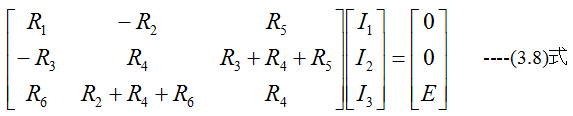
下記の計算条件において
| 記号 | 値 | 記号 | 値 |
| R1 | 30 | E | 12 |
| R2 | 30 | ||
| R3 | 19.999 | ||
| R4 | 20 | ||
| R5 | 10 | ||
| R6 | 10 |
| 記号 | 代数値 | VBA値 |
| I1 | 省略 | 0.171429292 |
| I2 | 省略 | 0.1714303 |
| I3 | 省略 | 0.00000302529 |
また、[例題3-2専用ソフト]は代数値は省略していますので、計算実行ボタンを押して、VBA解を求める必要があります。
具体的な計算にあたっては、下記の専用ソフトを使用すると便利です。
下記の[例題3-2専用ソフト]をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
[例題3-2専用ソフト]をダウンロードする。
４章：クーロンの法則とSIの電磁気の単位と磁界に行く。