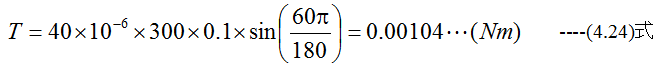クーロンの法則磁石はN極とS極がある。しかし磁気の計算をするため、一方の極が無限の遠方にあってその磁力が無視できるとして、N極またはS極だけ単独に存在すると考え、その磁性の根元を磁荷または磁気量という。
クーロンは実験から次の法則を考えた。
「2つの磁極間に働く吸引、反発力は磁極の強さの積に比例しその間の距離の２乗に反比例する。」
すなわち、２つの磁極の強さをM1、M2、その距離をRその力をF、比例定数をKとすると
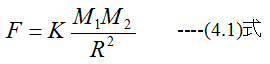
となります。(4.1)式において、力Fの単位はN、距離Rの単位はmとすべきでしょう。磁荷または 磁気量の単位はどうすべきか？
MKS単位系では以下の条件を満足するように決定されます。
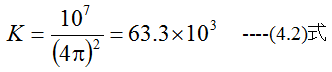
(4.1)式と(4.2)式を満足する磁荷または磁気量の単位をウェーバ(Wb)と定義します。
(4.1)式と(4.2)式は実験的に確認された定義式ですが、いくつかの疑問が生じます。
（１）磁力とは何か？N極またはS極だけ単独に存在可能なのか？
磁力は物体の原子内に円形電流が存在するためという磁気電子説が認められています。円形電流は磁気モーメントを発生しますが、N極とS極セットとなり単独で存在することはありません。
（２）なぜ(4.2)式のような定数を定義したか？
全立体角は4πであり(4.1)式はRの２乗項があるため、4πの２乗で割って単位立体角に変換したと思われます。10の7乗は日常的に使用するアンペア(A)の桁数合わせのためと思われます。
（３）かってに比例定数の値を定義して問題はないのか？
SIの電磁気の単位において、ひとつだけ比例定数の値を定義可能です。その唯一が(4.2)式の定数です。
SIの電磁気の単位SIの電磁気の単位表を下記に示します。
| 名称 | 記号 | 次元 | 物理量 |
| アンペア（SI基本単位） | A | A | 電流 |
| クーロン | C | A·s | 電荷・電気量 |
| ボルト | V | J/C = kg·m2·s−3·A−1 | 電圧・電位 |
| オーム | Ω | V/A = kg·m2·s−3·A−2 | 電気抵抗・インピーダンス・リアクタンス |
| オーム・メートル | Ω·m | kg·m3·s−3·A−2 | 電気抵抗率 |
| ワット | W | V·A = kg·m2·s−3 | 電力・放射束 |
| ファラド | F | C/V = kg−1·m−2·A2·s4 | 静電容量 |
| ファラド毎メートル | F/m | kg−1·m−3·A2·s4 | 誘電率 |
| 逆ファラド（ダラフ） | F−1 | kg1·m2·A−2·s−4 | エラスタンス |
| ボルト毎メートル | V/m | kg·m·s−3·A−1 | 電場（電界）の強さ |
| クーロン毎平方メートル | C/m2 | C/m2= m−2·A·s | 電束密度 |
| ジーメンス | S | Ω−1 = kg−1·m−2·s3·A2 | コンダクタンス・アドミタンス・サセプタンス |
| ジーメンス毎メートル | S/m | kg−1·m−3·s3·A2 | 電気伝導率（電気伝導度･導電率） |
| ウェーバ | Wb | V·s = kg·m2·s−2·A−1 | 磁束 |
| テスラ | T | Wb/m2 = kg·s−2·A−1 | 磁束密度 |
| アンペア（アンペア回数） | A | A | 起磁力 |
| アンペア毎メートル | A/m | m−1·A | 磁場（磁界）の強さ |
| アンペア毎ウェーバ | A/Wb | kg−1·m−2·s2·A2 | 磁気抵抗（リラクタンス） |
| ヘンリー | H | Wb/A = V·s/A = kg·m2·s−2·A−2 | インダクタンス・パーミアンス |
| ヘンリー毎メートル | H/m | kg·m·s−2·A−2 | 透磁率 |
| （無次元数） | χ | - | 磁気感受率 |
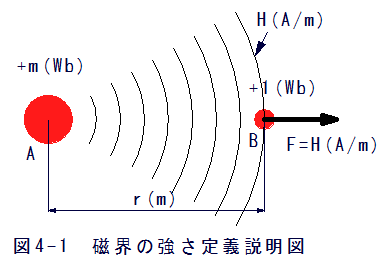
磁界の強さの定義図4-1において、Ａ点に+m(Wb)のN極をおいた場合、空間には磁界が発生します。
B点に単位N極（+1Wb)をおいた場合、クーロンの法則により反発力Fが発生します。
この反発力Fの方向を磁界の方向、力の強さをニュートン（N)単位で磁界の強さと定義します。
また、磁界の強さの単位を(A/m)または(AT/m)と定義します。
従って、図4-1における磁界の強さHは
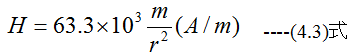
となります。
電気一般では、磁界の強さの定義を上記のように説明していますが、なぜ？こうなるか？の説明は省略しています。結果は正しいので丸暗記すれば問題ないのですが、だまされていないか？という疑問も生じます。
（１）N極とS極セットとなり単独で存在することはありません。
（２）なぜ？磁界の強さの単位がWb/m2でなくて、A/mなのか？
かなり説明を省略していますが、電流値は目で見えるものではありません。しかし電流を流すと磁界が発生することが確認されています。従って電流で生じる磁界の強さで電流値アンペア（A)は定義されます。
しかし、電流で発生する磁界は図4-1に示すような単純形ではありません。また直線電流とコイル電流でもかわります。磁界の強さは3次元ベクトルで与えられ、これを理解するにはベクトル解析の知識が必要となります。
詳細の説明は難しいのですが、(4.3)式が成立するように電流値は定義されます。
磁界も電流も発生する力ニュートン（N)で定義されることになります。単位の関係を整理すると
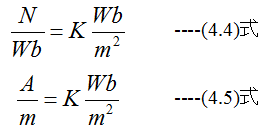
(4.4)式と(4.5)式から
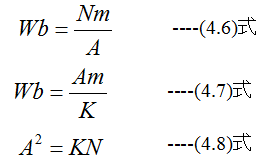
の関係が成立します。(4.8)式からKの値が決定すると、アンペア（A)の値が決定します。またウェーバ （Wb)の値も決定することがわかります。
（Kの値は唯一自由に定義できる定数です。）
例題4-120mWbと50mWbの磁極が5m隔てて置かれたとき作用する力はいくらか？
解答
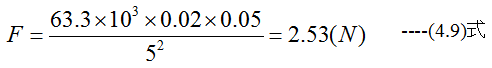
例題4-230mWbから30cm離れた点の磁界はいくらか？
解答
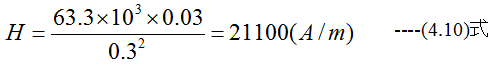
例題4-3磁界に30μWbの磁極を置いたとき、これに働く力が0.6mNであればその磁界はいくらか？
解答
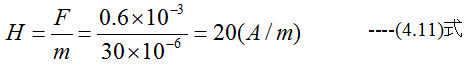
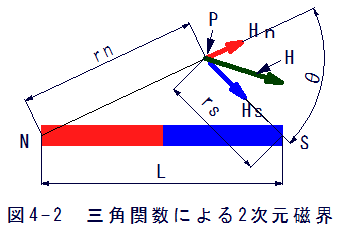
三角関数を使用した2次元磁界の計算式図4-2にしめす条件において磁極の強さをm下場合、以下の関係式が成立します。
NP方向分力Hnは
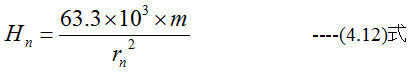
SP方向分力Hsは
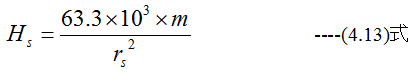
P点での合成磁界Hは
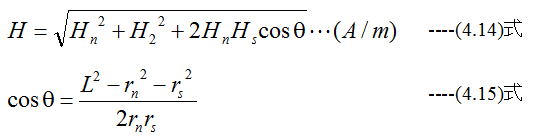
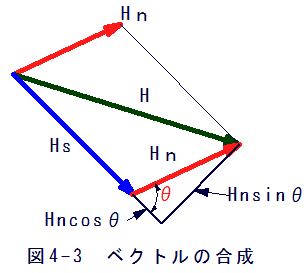ベクトルの計算はベクトル解析の手法を適用したほうが、スマートに計算できますが、上記
の関係式は三角関数のみで証明できます。ベクトルの合成は図4-3から
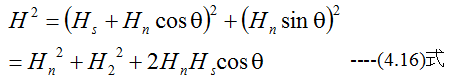
となります。
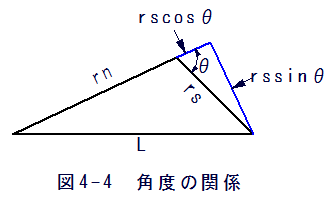また、図4-4から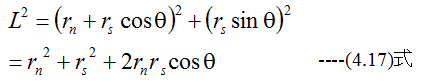
となります。(4.16)式と(4.17)式から(4.14)式と(4.15)式への変換は容易です。
三角関数法は視覚的に理解しやすいですが、手順は一定でなくパズル的です。
例題4-4長さが0.4mで、磁極の強さが225μWbも磁石のN極から0.5m、S極から0.3mの点の磁界の強度を求めよ。
解答
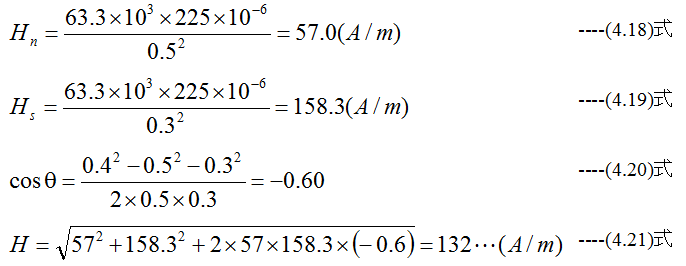
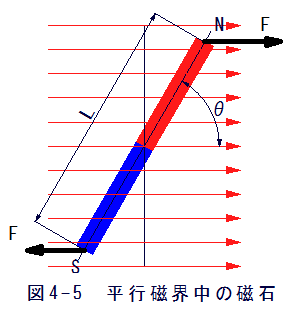
平行磁界中の磁石図4-2にしめす条件において磁極の強さをm下場合、以下の関係式が成立します。
図4-5に示すように平行磁界中に磁石をおくとトルクTが発生します。
磁界をH、磁石の強さをmとすると、N極とS極で発生する力Fは
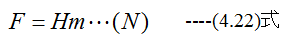
従って、発生するトルクTは
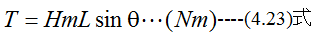
となります。
例題4-5300(A/m)の平行磁界に強さ40μWbの長さ10cmの磁針を磁界と60度の傾きで置かれたときのトルクはいくらか？
解答
５章：磁力線と磁気誘導に行く。