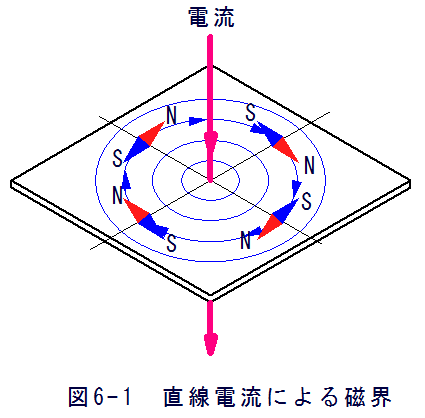
無限に長い直線電流が生じる磁界図6-1に示すように直線電流のまわりに小磁計（コンパス）をおくと円形の磁界が生じることが確認できます。
磁界の方向は電流の向きに右ネジをおいて、ネジを回す方向に磁界の方向が決定します。
これを「右ねじの法則」といいます。これは実験的に確認される法則です。
磁力線は電線を中心に同心円に生じます。電線からR(m)離れた点の磁界の強さHは
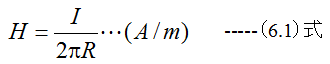
となります。（6.1）式を変形すると
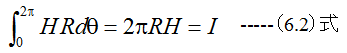
となります。（6.2）式は磁界Hを1周線積分した式であり、積分の結果がゼロにならず電流Iになることを示しています。これは1周して元の位置に戻っても値が一致しないことを示しており、物理的なポテンシャルエネルギーが定義できないことを示しています。
数学的には、スカラーポテンシャルが定義できないことを意味しています。
また、（6.1）式はアンペアーの法則とビオ・サバールの法則から証明することも可能ですが、証明の過程が複雑なため説明は省略します。
例題6-1100Aを流した直線電流から50cm離れた点の磁界の強さはいくらか？
解答
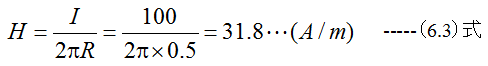
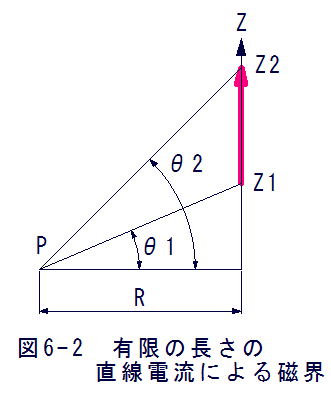
有限の長さの直線電流で生じる磁界図6-2に示すようにZ1からZ2の有限の長さで生じる磁界の強さは
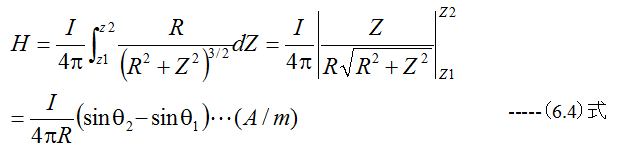
となります。（6.4）式はアンペアーの法則とビオ・サバールの法則から導くことができ ますが、複雑なので証明は省略します。
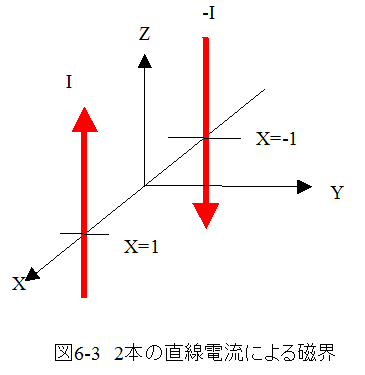
2本の直線電流による磁界図6-3の直線電流による磁界に示す条件での磁界の強さの 式（6.1）式から
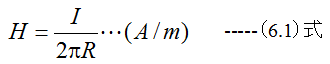
（6.1）式は円周方向の磁界を求める式であり、これを X,Y,Zの3次元ベクトルの式に変換すると
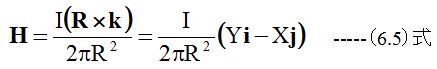
となります。XとY方向成分は
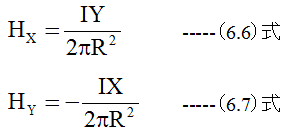
となります。図6.3に示す2本の直線電流による磁界は下記式となります。
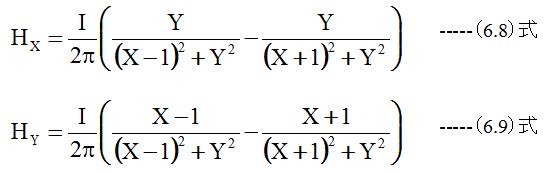
となります。磁界の強さは
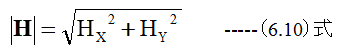
となります。しかし、グラフ化はうまくできません。（6.8）式と（6.9）式はセットであり、この値を2次元平面上に表現するのは難しいの です。磁界の強さは描くことができますが、符号が消えてしまうため、表現としては不十分となります。
そこでスカラポテンシャルを用いて表現したくなりますが、直線電流が作る磁界は磁位（ポテンシャルエネルギー）が定義できません。
そこでスカラポテンシャルのかわりにベクトルポテンシャルを計算することになります。1本の直線電流が作る磁場のベクトルポテンシャルは
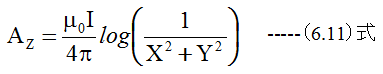
となります。2本の直線電流が作る磁場のベクトルポテンシャルは
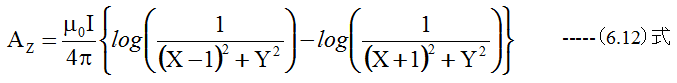
となります。簡単化のため
としてグラフ化すると1本の場合
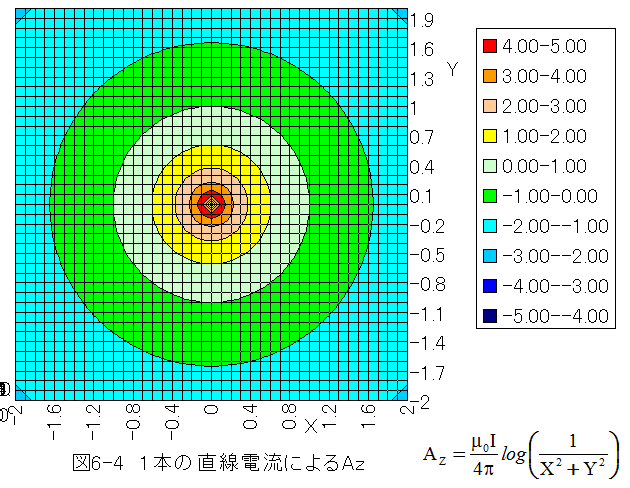
ＥＸＣＥＬ計算表は下記で参照できます。
「直線電流磁界1本」にいく。 2本の場合
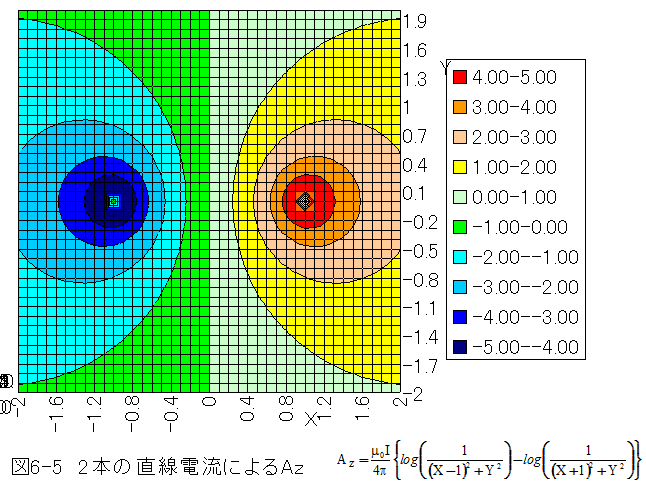
ＥＸＣＥＬ計算表は下記で参照できます。
「直線電流磁界2本」にいく。 となります。図6-4と図6-5において、等高線が磁力線と一致します。赤が正方向 （反時計まわり）青が逆方向（時計まわり）です。
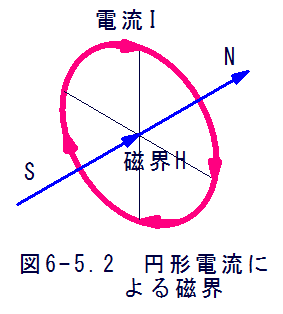
コイルの生ずる磁界図6-5.2に示すように円形の電流は磁石ににた磁界を発生します。この場合も実験的に右ネジの法則が適用できます。
「円形電流の磁界の方向は電流の方向が右ねじをねじる方向であれば、磁力線は右ねじの進む方向に貫く。」
いま電線を半径R(m)でN回巻いて、I(A)を流したときに生ずる磁界の強さHは
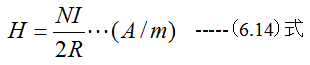
となります。
例題6-2実効直径1mに50回巻いたコイルを南北に置き、その中心に小磁計（コンパス）を置いたところ、その小磁計のN極が30°東方に傾いた。地球磁界の水平分力をHl=24A/mとし、電流の大きさを求めよ。
解答
電流による磁界Hiは
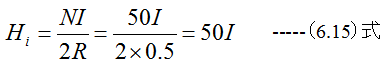
南北と東西の分力比から
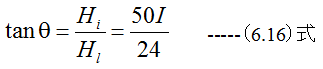
従って
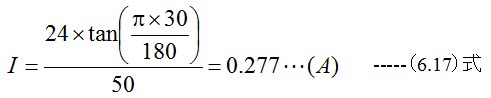
となります。
ソレノイドの磁界図6-6に示すように電線を密接して筒状に巻いたものをソレノイドというが、それに電流を流すと図6-6に示すような磁界ができます。この場合、右ネジの法則が適用できますが、右手母指の法則もわかりやすい。すなわち
「ソレノイドの電流の流れる周り方に右手母指以外の4指でにぎったときに、磁力線は母指の方向にある。」
図6-6をみると電流を通じたソレノイドは全く同じ磁性があることがわかる。
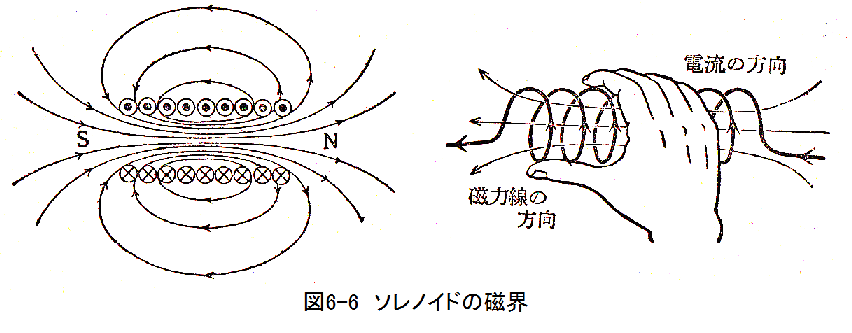
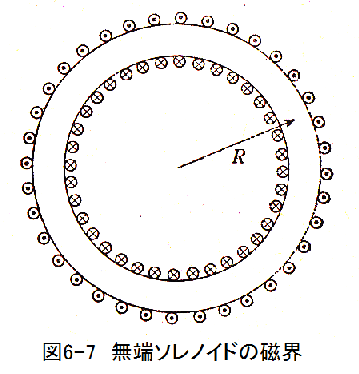
無端ソレノイドの磁界図6-7に示す無端ソレノイドは総数N回巻きであり、その直径と比較して十分大きな半径R(m)の円形である。これ に電流I(A)を流したとき、内部の磁界はほぼ均一で、磁界の強さHは
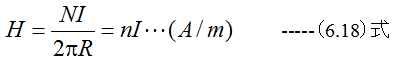
となります。（6.18）式において、nは1mあたりの巻き数となります。
また、図6-6に示すソレノイドにおいても長さが十分長いとき中央付近では同様に（6.17）式となります。
例題6-3直径8cmに2000回を巻いたソレノイドを平均直径80cmの円環に作って、これに50Aを流したとき、そのソレノイド中の磁力線の総数は何本か？
解答
電流による磁界Hは
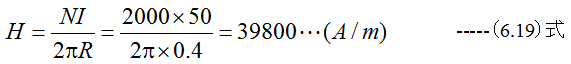
磁力線の数の定義はあいまいですが、ここでは1（A/m)で1m2あたり1本とするならば
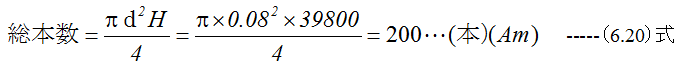
アンペアーの法則アンペアーは天才的な方法で種々の実験を行い、電流と磁場の相互作用の基本法則を確立しました。
アンペアーの法則は下記が根本となっています。
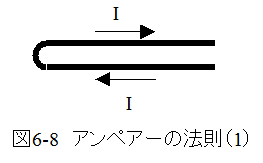
（１）平行に相接して逆向きに走る２つの相等しい強さの電流は互いに打消しあって外部に磁気作用を生じない。
（２）電流が流れている環状の線はあたかも磁石のような振る舞いをする。
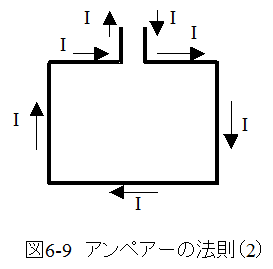
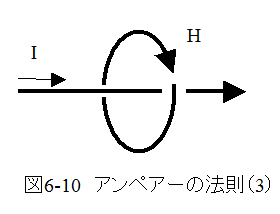
（３）図6-9において、電流の方向に右ネジを回した時にネジの進む方向が磁石のN極であるかのように振舞う。
上記の（３）を言い換えると図6-10に示すように「電流Iの方向に右ネジを回す時に、回す方向が磁場の方向と一致する。」となります。
コイル電流の法則アンペアーはさらに下記に法則を見出しています。
（１）電流が平面上の曲線にそって流れる時、この面上の磁位（ポテンシャル）はゼロである。
（２）あるコイルがP点において作る磁位は、P点からコイルをみた立体角に比例する。
上記の（２）を式にすると
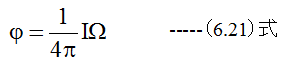
磁気双極子のポテンシャルは
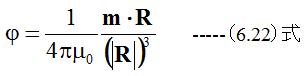
であり、（6.21）式と（6.22）式は等しくなります。従って
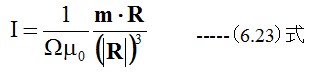
モーメントmと位置ベクトルRの成す角度をθとすれば
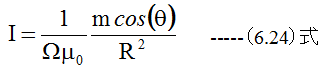
コイルが半径aの円形で、法線ベクトルｎと位置ベクトルRの成す角度をθとすれば
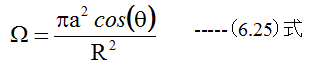
（6.24）式に（6.25）式を代入すると
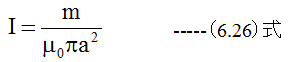
となる。（6.26）式をみればわかるように、電流Iが磁気モーメントmによって決まる。すなわち、コイル電流は磁気双極子と同じであり、磁気双極子に置き換えて考えることができます。
あるいは、磁石の磁気双極子は物質原子内の円電流によって発生するという説が有力となります。また、直線電流では、スカラポテンシャルを定義できませんでしたが、コイル電流ではスカラポテンシャルを定義できることになります。
(6.21)式を図6-5.2に適用すると
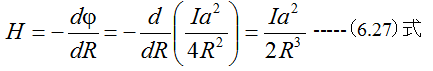
となります。ここでR→aの極限において
となります。（6.14）式と（6.28）式は巻き数Nをかけるだけで一致します。
磁石の中心部の磁界分布スカラポテンシャルの傾斜を計算すると磁界を求めることができます。磁界は3次元ベクトルであり、グラフ化しにくいの ですが、YZ方向は無視してX方向磁界を求めグラフ化すると下記のようになります。
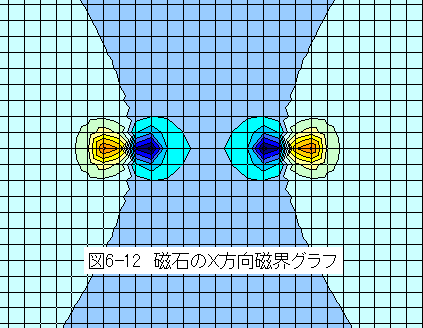
図6-12は磁石の両端のN極とS極の近傍で強く大きく変化しますが、磁石の中心付近では、均一な強度分布であることを示しています。
両端が存在しない無端ソレノイドでは、磁界が部分的に強くなることはなく、均一な強度分布となります。
（6.18）式はこの結果を単純な計算式で表現しています。（厳密に計算しようとするとかなり大変です。）
また、（6.18）式は十分長いソレノイドの中心付近に適用できます。