起磁力の定義いまN回巻きのソレノイドを作ってこれにI(A)の電流を流したときと2I(A)を流したときの内部の磁界の強さを調べると2倍になっている。また同じ長さに2N回巻いてI(A)を流してもｙはり同じところの磁界は2倍になっている。そこで電流によって磁界を生じる能力を起磁力と名づけ、アンペアと回数の積アンペア回数（記号AまたはAT）をその単位に決めた。
磁束と磁束密度いまソレノイドの同形の木棒と鉄棒を作っていれてみる。木棒の場合にはそれを入れないときと磁力は全く同一であるが、鉄棒をいれてみると、磁力鉄塊を吸引する力はくらべようがないくらい大きくなることが実験でわかる。
起磁力が等しければ磁界の強さも等しいから磁力線も等しい。ところが鉄をいれると磁力が著しく強くなるからいままでの磁力線ではだめである。そこで磁力線の定義を改良してもよいのだが、別に磁線という新しい線を考え、その性質は磁力線と全く同じであるが、鉄その他磁性体のときにはその数を著しく増加させることにした。ところが、1本2本と数えるとはんぱになったときにこまるので計算する便宜上から、とても多くの磁線を束ねた磁束（記号Φ）を考え、1Wbの磁極から出る磁束の数を1Wbと定めたのである。磁束（記号Φ）は束であるので整数である必要はありません。
また磁束の方向に垂直の単位面積を貫く磁束を磁束密度と名づけ、その記号にBを使う。すなわちΦが貫く面積をA(m2)とすれば
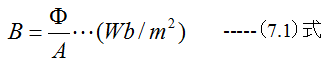
透磁率磁束密度をB、電流による磁界をH、比例定数をμとするならば
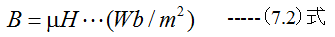
となります。この比例定数μを透磁率と名づけた。その単位は
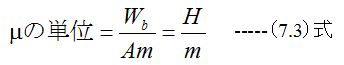
となります。(7.3)式のHはヘンリーと呼びます。 MKS単位系においては真空の透磁率μ0は
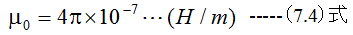
となり、物質中の透磁率μは
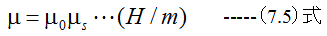
となります。(7.5)式のμsは物質の比透磁率といいます。比透磁率μsは空気、水、銅等多くの物質で1とみなして問題ありませんが、ニッケルは180、コバルトは270、鉄は状態によって120〜20000と大きな値となります。
なぜこうなるのか？
比透磁率μsは実験的に求める定数であり、実験的にこうなるといえば鵜呑みにするきりありません。物質はプラスの電荷を持つ原子核とマイナスの電荷を持つ電子で構成されています。
電子が存在できる場所は自由ではなく、位置エネルギーと運動エネルギーが定められています。運動エネルギーとは電子の運動エネルギーであり、円形運動すれば円形電流により磁気双極子が発生するはずです。
しかし、多くの物質は電子核の電荷と電子の電荷がバランスして全体としては電荷をもちません。同様に磁気双極子のプラスとマイナスがバランスするように配置されるため、全体としては磁性を持たないと考えられます。
しかし、特定の元素（ニッケル、コバルト、鉄）は磁気双極子のバランスがとれておらず、磁性を示すと考えられます。
このバランスのとれていない磁気双極子が磁界中で複雑な挙動を示すと考えられます。
例題7-1空気中で400(A/m)の磁界での磁束密度はいくらか？
解答
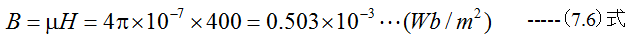
例題7-2切り口直径10cmの鉄環の平均直径が1mのものの表面に1000回コイルを巻き、15Aの直流を流し たとき、鉄環内部に磁束はいくらか？鉄の比透磁率は250とする。
解答
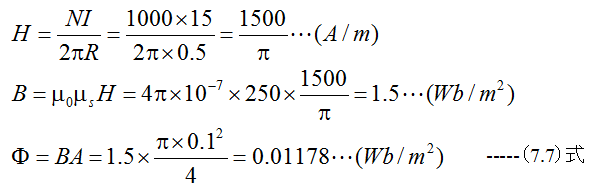
磁気回路閉磁路鉄心、すなわち鉄環のように鉄で閉じた磁束の通路があるときは、電気回路と同様に磁気回路として扱うことができます。
電気回路の電圧E（V）に対応して、起磁力F（A)となります。同様に電流I(A)に磁束Φ（Wb)が対応し、電気抵抗R(Ω）に磁気抵抗Rm（Wb/A)が対応、固有抵抗ρ（Ω）に透磁率μ(H/m)が対応します。そして以下の関係式が成立します。
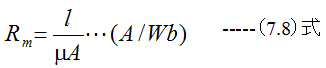
(7.8)式においてAは磁路（鉄心）の断面積、ｌは長さです。そして電気回路と同様に
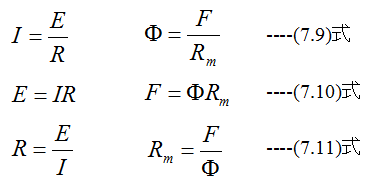
が成立します。
磁気抵抗の直列結合ｎ個の磁気抵抗Rmi(i=1,2,…,n）を直列結合した場合の合成抵抗Rmは
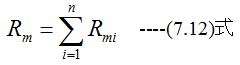
となります。
磁気抵抗の並列結合ｎ個の磁気抵抗Rmi(i=1,2,…,n）を並列結合した場合の合成抵抗Rは
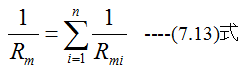
となります。
磁気回路の注意点電気回路の漏洩電流は数万分の1という無視して差し支えない値ですが、磁気回路の漏洩磁束は無視できない値となり概略計算であることを理解する必要があります。
電気回路の抵抗値は温度依存性はありますが、電流の大きさに大きく依存しません。これに対して磁気回路は磁束Φにより磁気抵抗Rmが大きく変化します。
磁路（鉄心）の断面積をAとして
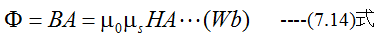
の関係が成立しますが、比誘電率μsが一定ならば、磁束密度Bは磁界Hに比例するはずです。しかし実際には複雑なカーブとなります。
これは、磁気回路の計算精度を著しく劣化させます。しかもこの変化は理論的に求めることができず、検証には実験データが必要となります。
鉄のB-H曲線と比透磁率変化鉄は炭素、タングステン、クロム、コバルト、チタン、ニッケル、アルミ、銅、珪素等との合金となります。化合物との状態により磁化特性は大きく変化します。
以下に鉄のB-H曲線と比透磁率変化例グラフをしめします。
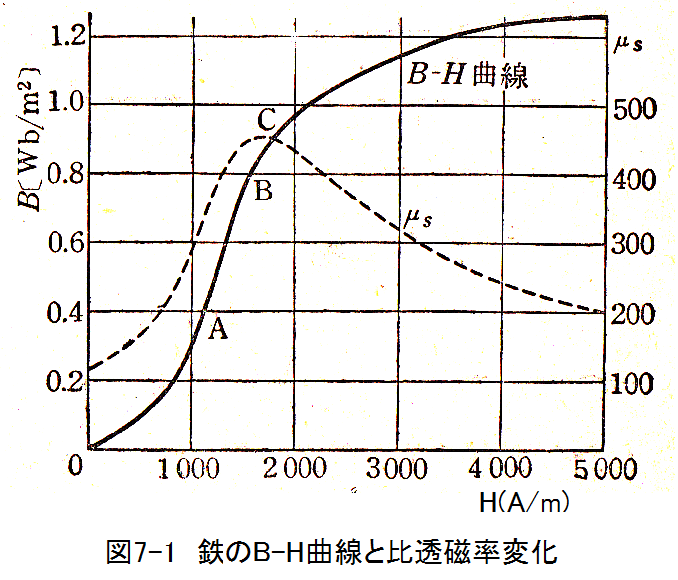
図7-1は鉄の磁化特性の一例で、横軸に磁界H、縦軸に磁束密度Bをとります。H=0のとき、B=0ですので初期磁性はゼロということになります。
磁界Hを上げていぐと1000(A/m)あたりから急速に磁束密度Bが上昇します。そしてH=3000(A/m)以上になると磁束密度Bの上昇は穏やかになります。
また、磁界Hを飽和状態から下げた場合は、ヒステリシスが発生し、上昇時と下降時のカーブが一致しません。
比誘電率μsはB-H曲線の傾きに比例します。このため比誘電率μsは一定値とならず図7-1に示すような複雑なカーブとなります。しかも、上昇時と下降時でヒステリシスが発生します。
これらの誤差を考慮した正確な計算はほとんど困難といっても過言ではないでしょう。
なぜ鉄はこのような複雑な特性を示すのでしょう？
有力な説は鉄原子の磁気双極子のアンバランス説です。鉄は原子内部にバランスがとれていない磁気双極子を持つ。通常の鉄は磁気双極子の方向がバラバラに固体化しており、全体としては弱い磁性を示す。これに外部から磁界が加わると一定の磁界強度以上で磁気双極子が動き出し、磁界の方向にそろってしまう。
雪崩現象と同じで一度雪崩が発生すると連鎖反応によって急激に磁束密度が上昇することになります。連鎖反応がおこった後は、磁界強度をさらに上げても方向がそろっていない磁気双極子はあまり残っていないことになります。従って一定に磁界強度以上ではB-H曲線は飽和することにないます。
また、バラバラの磁気双極子が磁界の方向にそろうためには、鉄原子が内部で回転する必要があります。この回転のしやすさ、しにくさは原子間結合の状態によって異なることになります。
純鉄や珪素鋼は回転しやすく、磁鉄鉱やフェライトは回転しにくいとかんがえられます。この回転しにくさからヒステリシスが発生するとおもわれます。永久磁石ではステリシスが大きい必要があります。
例題7-3切り口直径10cmの鉄環の平均直径が1mのものの表面に1000回コイルを巻き、15Aの直流を流したとき、鉄環内部に磁束はいく らか？鉄の比透磁率は250とする。磁気抵抗から計算せよ。
解答
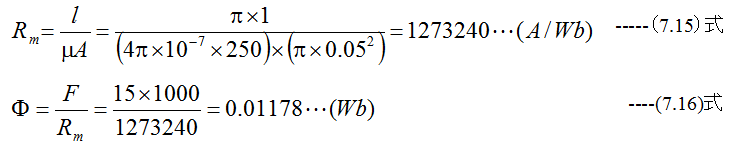
例題7-4断面積3cm2で平均長さ46cmの鉄環に幅1cmの切れ目をいれ、そこに0.45mWbの磁束を通じるには、1000回巻きのコイルに 何Aの電流を通すべきか？ただし、鉄の比透磁率は260とする。
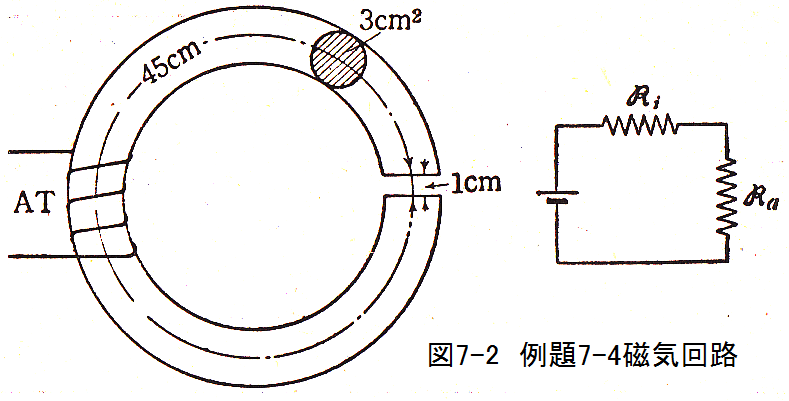
解答
直列の磁気抵抗Rmは
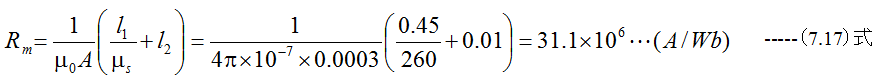
巻き数をNとした場合、必要な電流Iは
電磁石の吸引力
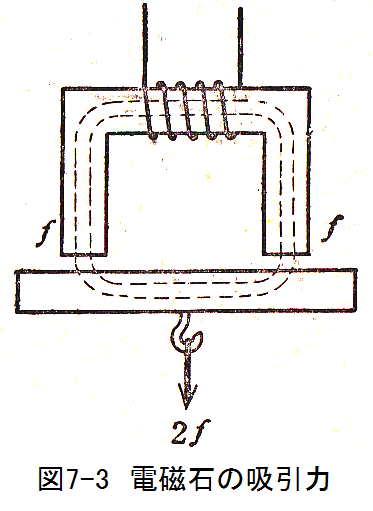
図7-3に示す電磁石は電流を流したとき強力な磁石になり、電流をきればただちに磁力が消失するものが望ましい。軟鉄はこの性質があるので広く利用されています。
さて、電磁石の吸引力はどのように計算すればよいか？
クーロンの法則から
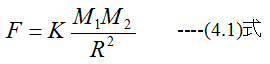
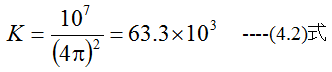
電磁石の断面積をAとして(4.1)式と(4.2)式は以下のように変形できます。
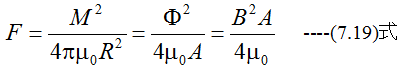
吸着面は2個あるので吸引力は2Fとなります。
例題7-5図7-3に示す電磁石において、断面積が10cm2で磁束が0.9mWbであるとき吸引力は何Nか？
解答
ヒステリシス
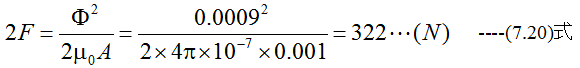
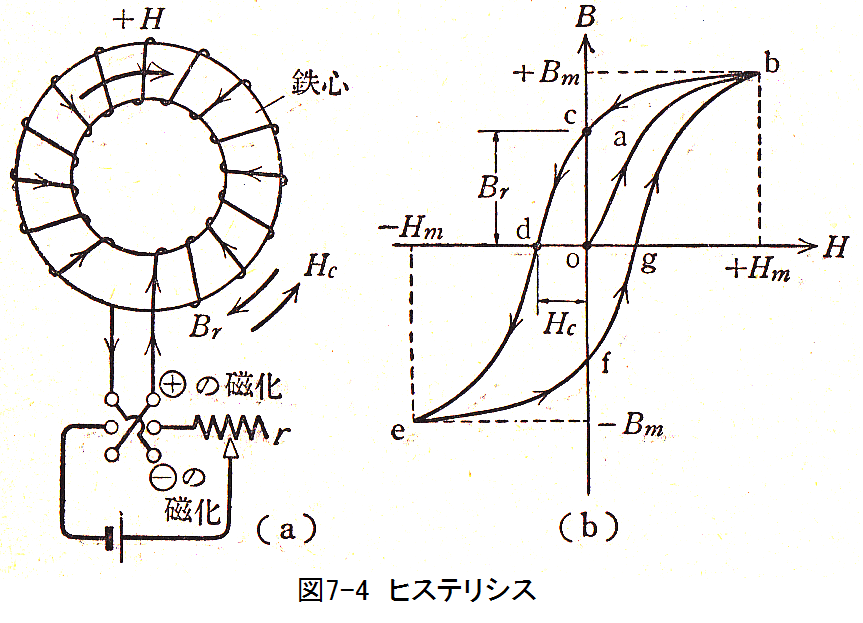
図7-4(a)に示すように鉄心にコイルを巻き、まず電流を徐々に増加してプラスの磁化力を加え、＋Hmとすれば、鉄心の磁束密度は徐々に増加してBmとなるが、あるところからBの増加割合が減ってくる。この現象を鉄が飽和したという。磁化力とは磁路の単位長さ当たりの起磁力である。
さて、次に磁化力を徐々に減ずると、ある鉄ではBの値は先に電流を増加したときの値より多くなり、電流をゼロとしてもBはゼロにならずある値を保つ。この現象を鉄にヒステリシスがあるといいます。この電流がゼロのときのBの値Brを残留磁気といいます。
そこで、切り替え開閉器で電流の方向を反対にしてマイナスの磁化力を加え、ついにBをゼロにした値Hcを保持力という。さらに磁化力を-Hmとし、そこで電流を減じゼロとし、切り替え開閉器を元に戻してまた電流を増して+HmにするとBはBmになる。
こうしてできた閉曲線をヒステリシス曲線といいます。そうして、この曲線で囲まれた面積Waがこの一循環にようするエネルギーを表わすのである。これを式で表わすと
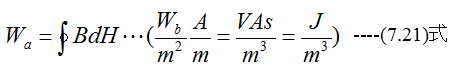
となります。（7.21）式の単位をみると、単位体積あたりのエネルギー(J)であることがわかります。線積分を一巡して値がゼロとならないことから、ポテンシャルエネルギーは定義できません。
一巡して消費されたエネルギーはどうなるのか？これは、磁気双極子の方向を変えるために生じた摩擦エネルギーになると考えられます。
したがって、ヒステリシス曲線の面積Waが大きな電磁石に交流電流を流すとエネルギーを消費して発熱することのなります。電磁石の鉄心用としては、Waが小さな軟鉄が適することになります。
逆に永久磁石は、残留磁気Brと保持力Hcができるだけ大きい方が望ましくなります。近似的にはｋを定数として
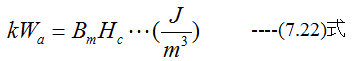
となりますので、残留磁気Brと保持力Hcの積で磁性材料の良否を判定します。
８章：電流の作用に行く。