磁誘導の発見
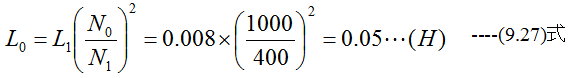
電流で磁気作用が発生するのだから、磁気から電流が生じまいかと考えるのは自然でファラデーがこれを発見した。
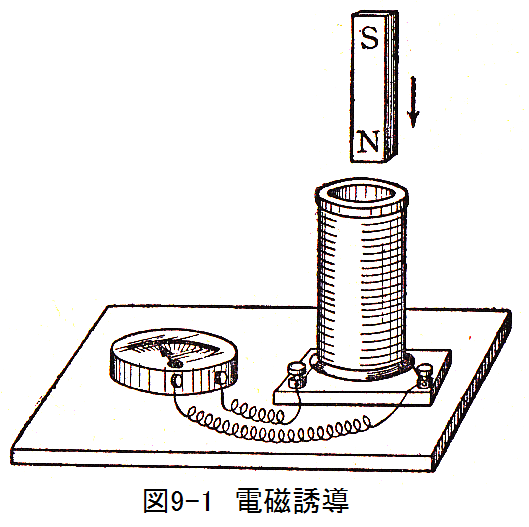
図9-1に示すようにコイルの両端に検流計つなぐ。このコイルに棒磁石を突込むと検流計の針が動いて電流が流れたことを示す。
ただし、それは磁石が動いているあいだだけで、磁石の運動が止まれば針の動きも止まる。
この現象を磁気誘導といい、この電流を誘導電流といいます。さらに実験を続けるとつぎのことがわかります。
（１）出し入れする速度が速いほど、検流計の指針の動きは大きい。
（２）N極をいれたときと、N極を引き出したときとでは誘導電流の方向が違う。またN極をいれたときとS極をいれたときも方向が違う。
（３）N極を入れたときとS極を引き出したときの速度が等しいと、検流計の指針の動き方も方向も等しい。
電磁誘導のモデル
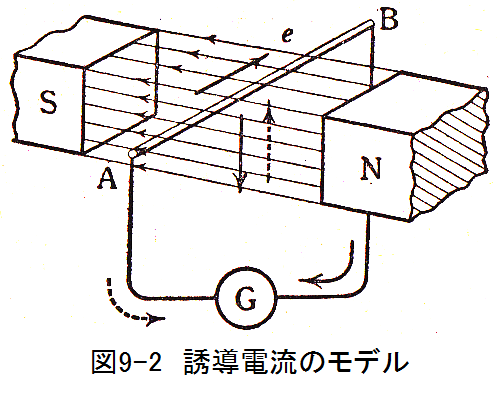
図9-2のように磁石の空隙内で導体を動かしても導体に起電力が誘起する。ただし、その運動の方向は電線の方向でも磁界の方向でも効果なく、電線と磁力線に直角ほ方向だけが役に立つ。それで導体が磁力線をきると起電力を誘起すると説明されます。
フレーミング右手3指の法則
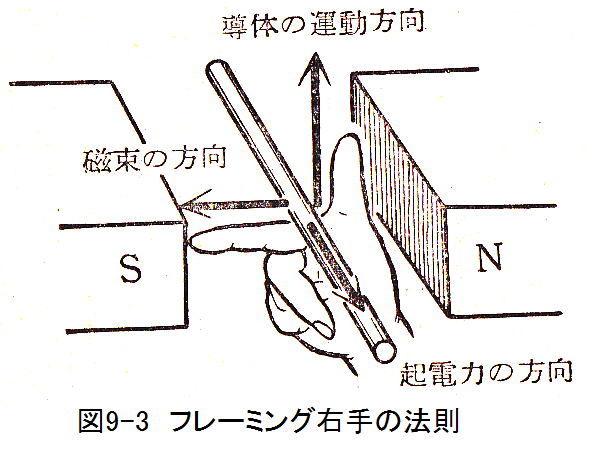
導体が磁束を切って誘起する起電力の方向を知るには「フレーミング右手3指の法則」が便利です。すなわち
「右手の親指と人差し指と中指を図9-3のよに直角に曲げ、親指を導体の運動方向、人差し指を磁束の方向に向けると起電力の方向は中指の方向に向かう。」
レンツの法則コイルの場合はレンツの法則の法則が便利です。
「誘導電流の方向は磁束の変化をもとの値に保つように生じる。」
すなわちコイルを貫く磁束が増すとき（たとえばN極をいれたとき）、誘導電流の方向は磁束を減ずるように生じる。磁束が減るときはその自足と同一方向の磁束を増すような誘導電流が流れます。
誘導電流の関係式誘導電流の大きさは
「磁束のきり方が毎秒１ウェーバ（Wb)のとき1ボルト（V)を誘起する。」
よってN巻きのコイルを磁束の変化をdΦ/dtとすると
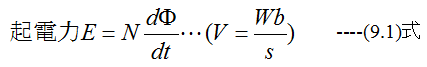
となります。（9.1)式から電圧Vは磁束Wbを時間sで割った値に等しいことになります。
例題9-1100巻きのコイルを貫く磁束が毎秒20mWbの場合、コイルに誘起する電圧はいくらか？
解答
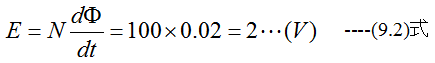
例題9-2自動車が時速72km/hの速さで東から西に走っているとき、長さ1mの鉛直アンテナには、地球磁気のためどんな方向に何Vを誘起するか？地球磁界の水平分力は0.24(A/m)とする。
解答
地球磁気の時速密度Bは
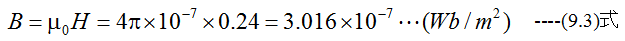
誘起起電力Eは長さをｌ、速度をｖとして
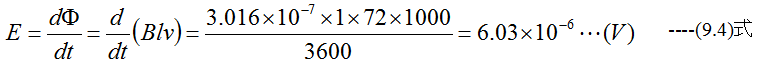
となります。起電力の方向はレーミング右手3指の法則から地面に向かう方向となります。
相互インダクタンス
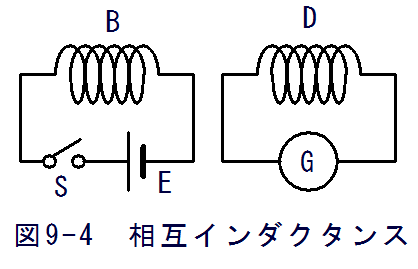
図9-4に示す回路でスイッチSを閉じるとコイルBに電流が流れますが、コイルDに接続された検流計が動きます。
これはとなりのコイルDに誘導電流が流れたことを示します。次にスイッチSを開けば一瞬だけ検流計は反対側に動きます。
いまBコイルの電流をdIb/dt（A)の割合で変化したとき、Dコイルに誘起する起電力がWd(V)とすれば
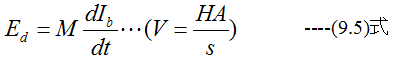
の関係にあります。この場合のMをBとDの２コイル間の相互インダクタンスといい、その単位をヘンリー（H)という。
この組合せでDコイルにdId/dt（A)の割合で電流を流したとき
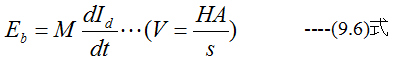
となります。このため相互インダクタンスといいます。
例題9-3図9-4でBコイルの電流を0から均等に5秒で100Aにしたとき、Dコイルに15mVが誘起した。このとき相互インダクタンスはいくらか？
また、Dコイルに誘導電流の方向に流しておき、それを10秒間に均等に100Aから0Aにしたとすれば、Bコイルに誘起する起電力はいくらか？またその方向ははじめの電流と同じか？反対か？
解答
相互インダクタンスは
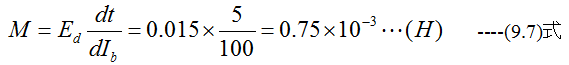
Bコイルに誘起する起電力は
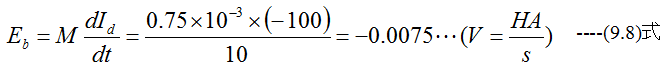
初めBコイルに左から右に電流が流れ、磁束も左から右に向かって増加したとする。このときDコイルに右から左に電流が流れたとします。
次にDコイルに右から左に電流を流したとすれば、Dコイルを貫く磁束は先の磁束とは反対方向にBとDコイルを貫きます。例題は電流を減らす方向に変化させるため、Bコイルの電流は初めの電流と反対になります。
自己インダクタンス誘導電流の起電力は自分のコイルにも誘起します。すなわち抵抗がR（Ω）のコイルの電流を毎秒I(A)の割合で増加にるにはIRのほかにEL（V)の電圧が必要となります。
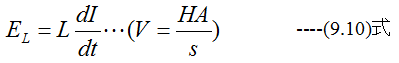
(9.10)式のLを自己インダクタンスといいます。その単位はヘンリー（H)となります。これは、電流を増加するにはコイルを貫く磁束も増加する ので、その増加磁束がコイルをきるからです。
インダクタンスは次ようにいえます。
「電流変化が毎秒1Aの割合のときは、誘起する起電力のボルト数とインダクタンスのヘンリー数は等しい」
また
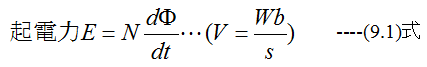
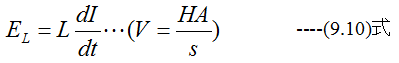
(9.1)式と(9.10)式から
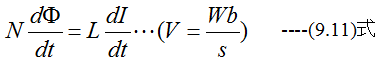
あるいは
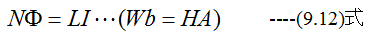
が成立します。これはつぎのようにいえます。
[コイルに1Aが流れているとき磁束の鎖交数とインダクタンスのヘンリー数は等しい」
端ソレノイドのインダクタンス
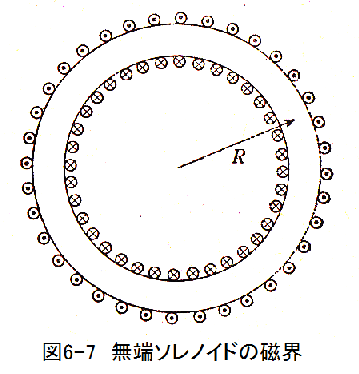
図6-7に示す無端ソレノイドは総数N回巻きであり、その直径と比較して十分大きな半径R(m)の円形である。これに電流I(A)を流したとき、内部の磁界はほぼ均一で、磁界の強さHは
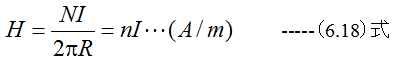
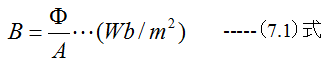
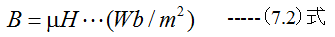
(9.12)式、（6.18）式、（7.1）式、（7.2）式から
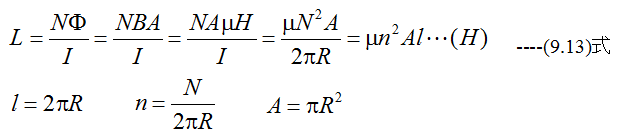
（9.13）式を得ることができます。
この環状コイルを切り開いて直線にした有限長さのソレノイドでは、Lは環状よりも減少する。その減少率を長岡係数といい半径と全長に関係する。
例題9-4ある500回巻きのコイルに5A流れたとき、これを貫く磁束が36μWbだとすれば、このコイルの自己インダクタンスはいくらか？ただし、漏洩磁束はないとする。
解答
(9.13)式から
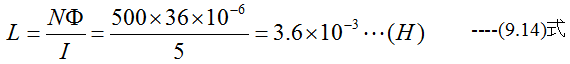
例題9-5直径10cm、長さ60cm、巻き数300回で透磁率0.0006の鉄心を有するインダクタンスはいくらか？ただし、長岡係数は0.94とする。
解答
(9.13)式から
相互インダクタンス
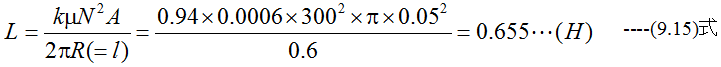
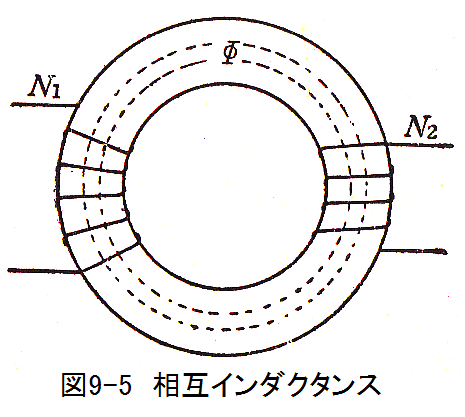
いま図9-5に示すように同一鉄心にN1巻きとN2巻きとの２つのコイルを巻き、第１のコイルにI1(A)を流したとき、鉄 心にΦ(Wb)の磁束が貫くとすれば、第１のコイルの自己インダクタンスは
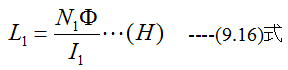
です。次に第２コイルにI1（A)を流したとすれば磁気抵抗の式から
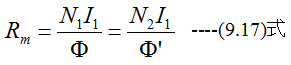
ゆえに
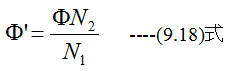
です。したがって第２コイルの自己インダクタンスは
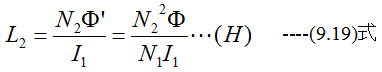
また、相互インダクタンスは
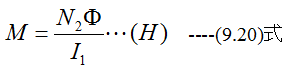
です。L1とL2の積を求めると
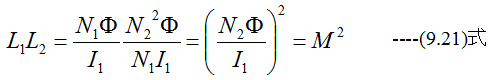
となります。そこで一般化して
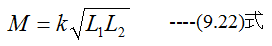
とします。(9.22)式のkを結合係数といいます。漏洩磁束がゼロのときk=1となり、漏洩が ある場合は1より小さくなります。
例題9-6自己インダクタンスが40mHと90mHのコイルの相互インダクタンスが48mHであれば結合係数はいくらか？
解答
インダクタンスの直列結合
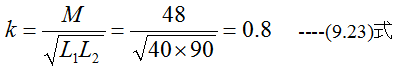
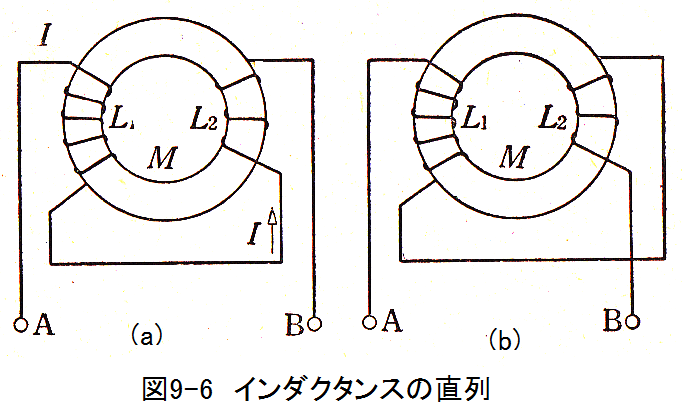
図9-6の(a)のように接続したときAB間のインダクタンスL0は
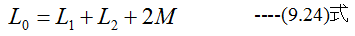
となります。図9-6の(b)のように接続したとき相互インタクタンスは、それぞれ逆方向に作用するため
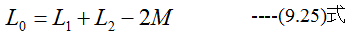
となります。
例題9-7同一の鉄心に1000回のコイルを巻いて、一端から400回のところでタップをだして2つのコイルに区分した。いま400回の分の自己インダクタンスが8mHだとすれば、残りの部分および全体の自己インダクタンスはいくらか？ただし漏れ磁束はないものとする。
解答
600回分の自己インダクタンスは
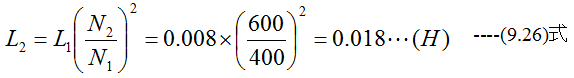
1000回分の自己インダクタンスは
１０章：直流発電機に行く。