任意の波長における光学ガラスの屈折率任意の波長における光学ガラスの屈折率は関数近似式を用いて計算します。一例としてオハラ光学の関数近似式は
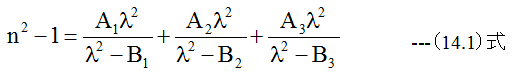
となります。波長λの単位はμmを使用します。
なぜ？このような形の近似式を用いるのか？これは、光の不思議と応用 ８章：屈折率の波長特性
８章：屈折率の波長特性に行く。を参照願います。８章：屈折率の波長特性（8.11）式の粘性係数γ＝0とした場合の関数形に一致することがわかります。
オハラ光学ガラスの定数表は下記を参照願います。
「オハラ光学ガラスの定数表」にいく。 光学ガラスの種類は119種類もあることがわかります。
ガウス・ニュートン法による屈折率の関数近似（16.1）式は非線形の関数形をしており、関数近似には若干の工夫が必要となります。誤差関数Eを以下のように定義します。
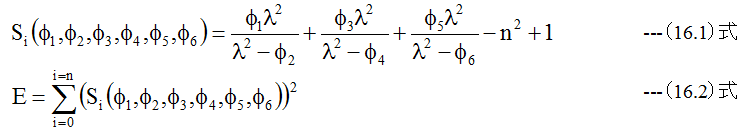
ここでΔφ1、Δφ2、…、Δφmだけ変化させたとき
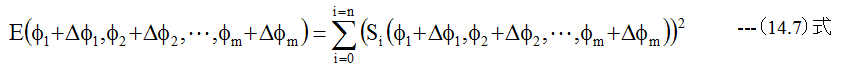
となります。（14.7）式をφ1、φ2、…、φmで偏微分した値がゼロとなる条件式を作成すると
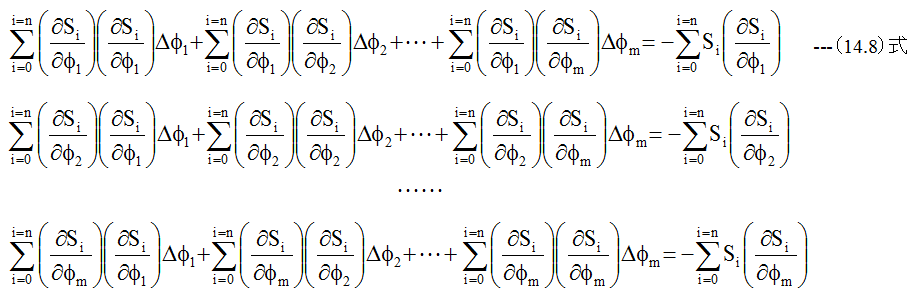
（14.8）式はm元の連立1次方程式であり、これからΔφ1、Δφ2、…、Δφmの値を求めることができます。
φ1、φ2、…、φmの初期値は不明ですが、通常初期値をゼロとしてΔφ1、Δφ2、…、Δφmの値を求めφ1、φ2、…、φmの値を順次補正することにより、φ1、φ2、…、φmの値は最適値に収束します。
光学ガラスの関数近似C#、WPFソフト光学ガラスの関数近似にC#、WPFアプリケーションを適用してみました。
完成ファイルは以下からダウンロードできます。
ダウンロード後は解凍してから使用してください。
[光学ガラスの関数近似C#、WPFソフト]をダウンロードする。解凍すると「Glass2」フォルダーがあります。
フォルダー内の「Glass2.sln」をダブルクリックすると「Express 2012 for Windows Desktop」が起動して、プログラムの修正・デバッグが可能です。
フォルダー内の「Glass2.exe」をダブルクリックすると実行プログラムが起動して、光学ガラス組合せ最適化計算が可能となります。
フォルダー内には、操作説明用データファイル
「屈折率定数表(オハラ値）.txt」
「屈折率定数表（初期不明時）.txt」
「屈折率少data.txt」
があります。
操作例1「屈折率定数表(オハラ値）.txt」を使用します。数値はオハラのホームページから入手可能です。
（１）「Glass2.exe」をダブルクリックします。
（２）メニューの「開く」を選択します。
（３）「屈折率定数表(オハラ値）.txt」を開きます。
（４）操作の「最適化計算実行」を選択します。
（５）計算結果数表が表示されます。
（６）メニューの「保存」を選択選択すると計算結果数表をタブ区切テキスト形式で保存できます。
・このサンプル事例においては、関数近似の定数は正確な値が設定されており、定数の値はほとんど変化しません。
・正確な初期値が設定してある場合は、収束演算繰り返し回数は少なくて済みます。最適化探索回数は、最初から誤差標準偏差判定値を満足しますので、探索を繰り返すことはありません。
・計算は短時間で終了します。
・オハラ公開の関数近似の定数の値は全て、数値の有効桁数の範囲で正確であることが確認できます。
操作例2「屈折率定数表（初期不明時）.txt」を使用します。関数近似の定数の値が不明の場合、最適値の探索が必要となります。初期値は全光学ガラスの平均値としました。
（１）「Glass2.exe」をダブルクリックします。
（２）メニューの「開く」を選択します。
（３）「屈折率定数表（初期不明時）.txt」を開きます。
（４）操作の「最適化計算実行」を選択します。
（５）計算結果数表が表示されます。
（６）メニューの「保存」を選択選択すると計算結果数表をタブ区切テキスト形式で保存できます。
・このサンプル事例においては、全ての光学ガラスの最適解が求まるとはかぎりません。
・初期値の条件によりますが、通常は近似誤差の大きい極値に収束します。このような場合、乱数を用いて初期値を変更します。
・乱数による初期値の変更は収束演算繰り返しの途中と最適化探索繰り返し時に実行されます。
・従って、収束演算繰り返し回数と最適化探索回数を大きくすると、最適解が求まる確率が高くなります。（ただし、演算時間は長くなります。）
・最適化演算に失敗してもメッセージの表示はありません。この場合、誤差Eの値に0が表示されます。
・光学ガラスの関数近似式は非線形であり、解は必ずしも1つとなりません。根気強い繰り返し演算が不可欠となります。
操作例3「屈折率少data.txt」を使用します。データ数が少ない場合や欠けがある場合の事例です。
（１）「Glass2.exe」をダブルクリックします。
（２）メニューの「開く」を選択します。
（３）「屈折率少data.txt」を開きます。
（４）操作の「最適化計算実行」を選択します。
（５）計算結果数表が表示されます。
（６）メニューの「保存」を選択選択すると計算結果数表をタブ区切テキスト形式で保存できます。
・このサンプル事例においては、屈折率不明の波長のセルには「-1」が設定してあります。マイナスの値または空欄のときデータ無しと判定します。
・データ数が3個の時、定数は3個決定され、データが4個の時定数は4個、データが5個の時定数は5個決定されます。
・サンプル事例においては、データ数が少ないので、誤差標準偏差判定値を厳しくし、収束演算繰り返し回数と最適化探索回数を大きく設定可能です。
感想：
（１）屈折率は波長に対して単調な減少曲線で、比較的簡単に関数近似が可能ではないか？と思ったのですが、思いのほか初期値設定が難しく、てこずりました。