誘電率は物理定数の一種ですが、反射率測定の結果から逆算することも できます。その原理について考えててみたいと思います。
反射と屈折の法則反射と屈折の法則については光の不思議と応用＿９章：反射と屈折の法則
９章：反射と屈折の法則に行く。で詳細を解説しています。
斜め入射での反射率の計算式（１）保存：数表データをタブ区切りテキスト形式で保存します。
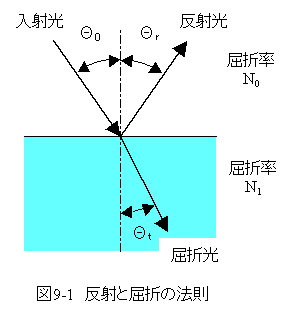
図9-1において、反射光の角度は
の関係があります。 また、屈折光の角度は
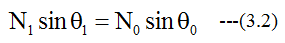
斜め入射の場合はS偏光（電場の振動方向が水平面と平行）とP偏光（電場の振動方向が水平面と直角） で反射率が異なります。
P偏光の反射率は
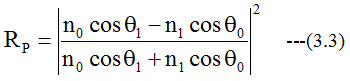
S偏光の反射率は
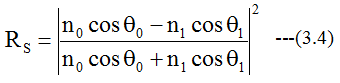
となります。ここではC#、WPFアプリを適用して計算してみたいと思います。
斜め入射での反射率計算プログラム斜め入射での反射率はEXCELの表計算でも可能です が、C#、WPFアプリケーションで作成します。
完成ファイルは以下からダウンロードできます。
ダウンロード後は解凍してから使用してください。
[斜め入射での反射率計算プログラム]をダウンロードする。解凍すると「reflection」フォルダーがあります。
「beam」フォルダー内の「reflection.sln」をダブルクリックすると「Express 2012 for Windows Desktop」が起動して、プログラムの修正・デバッグが可能です。
「reflection.exe」をダブルクリックすると実行プログラムが起動して、斜め入射での反射率の計算が可能となります。
操作説明（１）計算実行ボタンを押すと数表が作成されます。
（２）グラフ表示ボタンを押すとグラフが表示されます。
（３）戻るボタンで主画面に戻ります。
（４）再度計算実行ボタンを押して数表を作成します。
（５）メニューの「保存」を選択すると、数表をタブ区切りテキスト形式で保存できます。
（６）クローズボックスで終了します。
感想：
（１）斜め入射での反射率の計算において重要なパラメータは複素屈折率です。
（２）物体の複素屈折率が決定すると、斜め入射での反射率が全て決定されます。
（３）斜め入射での反射率特性から、物体の複素屈折率を決定するとこも可能です。
（４）複素誘電率は複素屈折率の自乗として求めることができます。
（５）従って、斜め入射での反射率特性から物体の複素誘電率を求めることができます。
（６）全ての物体は、斜め入射での反射率特性の測定が可能であり、全ての物体は固有の 複素誘電率を有することになります。
（７）複素屈折率の値をいろいろ変えて斜め入射での反射率特性を計算すると以下のことに 気づきます。
（８）物体の屈折率実数部の値が1に近いと反射率が小さくなる。
（９）物体の屈折率実数部の値が0に近づくと入射角度に依存しないで反射率が大きくなる。 （金属に近い特性を示す。）
（１０）物体の屈折率実数部の値が1と比較して大きいとき、垂直入射に対して反射率が 大きくなるが入射角度の依存性が大きい。（高誘電率物質）
（１１）物体の屈折率の虚数部が大きいと吸収による減衰が大きくなる。
（１２）全ての物質で複素誘電率は存在するのではないだろうか？