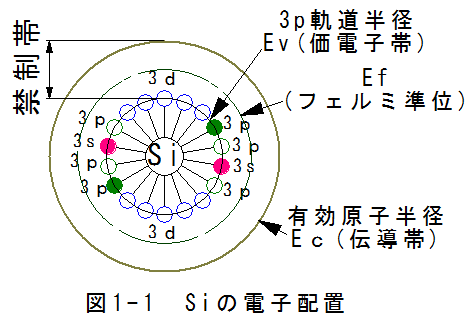
原子構造単独に存在する原子は原子核と核外電子から構成される。核外電子は定まった軌道に定まった数しかはいれない。したがって核外電子はとびとびの定まったエンルギーレベルしかとりえない。
内側の軌道は電子が一杯つまっていて、原子核との結びつきが強く外界とはほとんど作用しない。
すなわち、化学的性質に関係するのは、最外殻の電子でこれを荷電子と呼ぶ。
図1-1にシリコン(Si)の電子配置を示します。荷電子帯は2個の3s軌道と6個の3p軌道で構成され、電子が4個、空席が4個あります。
シリコン(Si）原子が集まって結晶を作る場合、となり合わせの原子と電子を1個ずつ共有して最外殻の電子が8個となって安定します。これを共有結合といい、ダイヤモンド構造となります。
充満帯、禁止帯、伝導帯原子が集まって、結晶を作ると、最外殻の電子のとり得るエネルギーレベルは、禁止帯をはさんで充満帯と伝導帯にわかれる。充満帯は共有結合により原子核を結びつけている電子がはいっているところで原子核との結びつきが強く普通の状態では電気伝導に関係しない。
しかし、周囲温度を上げたり、光を当てたりして充満帯の電子にエネルギーを与えると禁止帯の幅以上のエンルギーを得た電子は禁止帯を飛び越して伝導帯に上がる。
この伝導帯の電子がいわゆる自由電子で、電界の方向に移動して電気を伝導できる。
また、電子が飛び出した空席は電子を奪い取って新たな空席を作る。空席はプラスの電荷を持ち、電界の方向に移動して電気を伝導できる。
禁止帯は両者の間にあり、電子がとりえないエネルギーレベルでこれをギャップエネルギーという。
金属・絶縁物・半導体金属は最外殻の電子が通常の原子間結合距離で伝導帯に押し出される。このため絶対零度においても、伝導帯に自由電子が存在し、電界の方向に移動して電気を伝導できる。
金属と類似の特性を持つ物質として、グラファイトがあるが、これも六角結晶の結合により炭素原子の最外殻の電子4個のうち1個が伝導帯に押し出されるためである。
つぎに絶縁体としてダイヤモンドを例にとると禁止帯の幅が広く、ギャップエネルギーは6〜7eVもある。
常温に相当する電子の運動エネルギーは小さく、また可視光線の波長に相当する光量子のエネルギーは2〜2.5eVである。このため、ダイヤモンドは常温では伝導帯にほとんど自由電子が存在しないため、電気を通さず絶縁体となる。
GeやSiの単結晶も結晶構造はダイヤモンドと同じであるがギャップエネルギーが小さく、Geで0.7eV、Siで1.2eV程度である。したがって常温でも伝導帯に自由電子が存在し導電性を示す。常温で純粋なGe単結晶の比抵抗は60Ω・cm、Siの比抵抗は60kΩ・cm程度である。
フェルミレベル真性半導体において絶対零度では、最外殻の電子は充満帯にあり、伝導帯には1個もない。だんだん温度を上げていくと、禁止帯より大きいエネルギーを得た電子は充満帯に空席を残して伝導帯にあがる。結晶中には多数の電子があるから、エネルギーを得たものは伝導帯に上がり、またエネルギーを放出して充満帯に下がる現象を繰り返して、伝導帯と充満帯の電子の分布は一定温度で、ある平衡状態にある。
この確率分布を与えるのがフェルミーディラックの分布関数です。
フェルミーディラックの分布関数は任意のエネルギーEiにおける自由電子の存在確率fiを与えます。
（1.1）式において任意のエネルギーEi=フェルミレベルEfのときfi=0.5となります。また絶対零度近傍においてEi
トランジスタ回路入門は入門書の紙面の制約のためか？証明なしにフェルミーディラックの分布関数が記載されています。
フェルミーディラックの分布関数の証明については、「特設講座」私の考える半導体物理 ５章：フェルミーディラック分布関数
５章：フェルミーディラック分布関数に行く。を参照願います。
電子とホール純粋な半導体結晶の中で充満帯にいる荷電子がエネルギーを得て伝導帯に上がると自由電子となる。もともと原子は電気的に中性であったから、荷電子が1個去るよ後には電子1個分の正の電荷が残る。この正の電荷を電子が抜けた孔という意味でホールと呼ぶ。
半導体の結晶の両端に電極をつけて電圧をかけると、伝導帯の自由電子は正電極の方に移動して電流が流れる。また、ホールは負電極の方向に移動して電流が流れる。
電流を運ぶものという意味で電子とホールを総称してキャリアと呼ぶ。
真性半導体不純物を含まないGeやＳｉの単結晶では、電子が伝導帯に上がると必ず後にはホールができるから、電子濃度nとホール濃度pは等しい。このように両者の濃度が等しい半導体を真性半導体という。
さて、真性半導体の電子濃度nとホール濃度pはどのように計算すればよいか？
記号説明
Ev＝充満帯のエネルギーレベル
Ef＝フェルミレベル
Ec＝伝導帯のエネルギーレベル
Eg＝ギャップエネルギー
とします。
トランジスタ回路入門においては計算の誘導の説明がありますが、内容的にはうまく理解できません。
フェルミーディラックの分布関数は以下の条件で近似式にします。
E＞Eｃの時
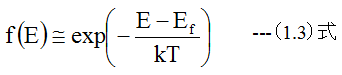
E
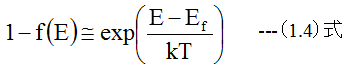
（1.2）式、（1.3）式、（1.4）式から以下の式が得られるとあります。
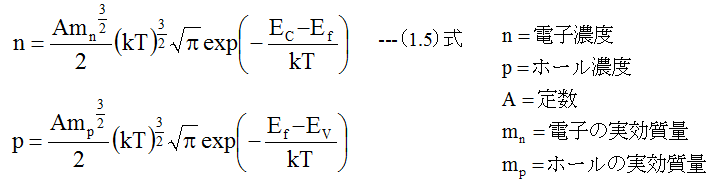
上記の説明において、状態密度関数N(E)は意味不明であるのと、（1.2）式、（1.3）式、（1.4）式から（1.5）式の結果は導くことができませんでした。
ただし、最終的な（1.5）式は他の検討結果と一致します。具体的な計算においては、（1.2）式、（1.3）式、（1.4）式は使用しません。計算は（1.5）式で行うため正しい結果がえられます。
最終的には、定数Aは実験式と比較して決定されます。実験式の関数形は確定しており、理論式と実験式の関数形は一致しなければなりません。
理論式のモデルが間違っていても、実験式に合わせこむため正しい値を計算できます。
理論式の検討は「特設講座」私の考える半導体物理 ６章：半導体中のキャリア濃度
６章：半導体中のキャリア濃度に行く。で行っており、最終的な（1.5）式は一致することが確認できます。
pn積（1.5）式から
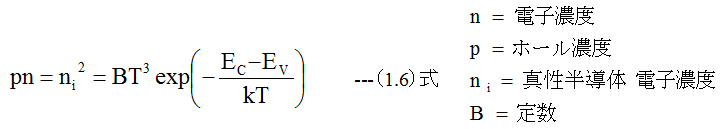
の関係式を得ることができます。すなわちpn積はフェルミレベルEfに関係せず、温度TとギャップエネルギーEg=Ec-Evのみの関数となります。
n型半導体周期律表から第5属の原子、すなわち、5個の荷電子を持つリン（Ｐ）、砒素(As)、アンチモン(Sb)等をGeやSiに極微量加えて単結晶を作るとこれらの原子はGeやSiに性質が似ているため結晶構造を乱すことなく、GeやSiの原子に置き換わってしまう。
これらの不純物の原子は5個の荷電子を持っているため、4個の荷電子は共有結合に使われるが残り1個はあまってしまう。この1個の荷電子は原子と結合していないため自由電子となる。
すなわち、5族の不純物は原子1個あたり1個の自由電子を作るが、後にホールを残さない。このような半導体では、電子の濃度がホールの濃度よりはるかに多くなる。この5族不純物をを含む半導体を負の電荷を持った電子濃度が高いという意味でn型半導体と呼び、5族不純物原子をドナーと呼ぶ。
p型半導体n型半導体に対応して、3族の原子、すなわち3個の荷電子を持つアルミニウム(Al)、ガリウム(Ga)、インジウム(In)等をGeやＳｉに加えて単結晶を作ると、ホール数が電子数より多いp型半導体ができる。
この場合は、共有結合において電子が1個不足し、ホールができる。この３族の不純物原子をアクセプタと呼ぶ。
不純物半導体のエネルギーレベルn型半導体すなわちn型の不純物第5属の原子を入れた場合、１個の荷電子があまりはじきだされます。このため不純物原子はプラスに帯電し、荷電子との引力が発生します。このため、原子核との引力を持たない伝導帯のエネルギーレベルよりも僅かに小さくなります。
p型半導体すなわちp型の不純物第3属の原子を入れた場合、１個の荷電子が不足します。このため不純物原子は不足した電子をおぎないマイナスに帯電します。このため充満帯のエネルーレベルよりも僅かに大きくなります。この値は
Geのエネルギーレベルの変化量＝0.01 eV
Siのエネルギーレベルの変化量＝0.05 eV
となります。この値は小さいため通常は無視することができます。
不純物半導体のフェルミレベルフェルミーディラックの分布関数は真性半導体に熱エネルギーが加わった場合の、電子の存在確率を与えます。フェルミレベルは充満帯と伝導帯の中点となります。
不純物半導体は絶対零度でも電子またはホールが存在することになります。このため、不純物半導体のフェルミレベルをどのように定義するか？
仮に電子の存在確率が0.5となるエネルギーレベルを不純物半導体のフェルミレベルと定義しても物理的な意味は難解です。
不純物半導体のフェルミレベルを使用しないで理論の展開はできないだろうか？（実際には、計算の都合上、不純物半導体のフェルミレベルを使用します。）
不純物半導体のキャリア濃度不純物濃度に関係せずに（1.6）式は成立します。
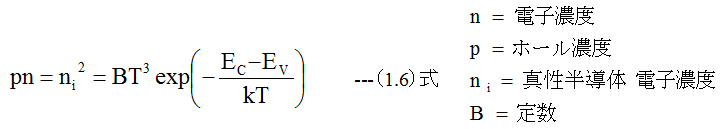
不純物濃度Ndの半導体の電子濃度をnd、ホール濃度をpdとすると
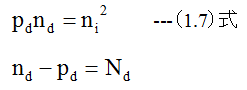
（1.7）式を解くと
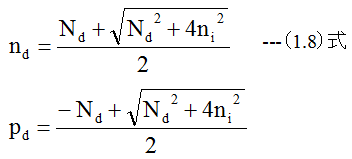
となります。
電界による電気伝導半導体中のキャリアすなわち、電子やホールは熱エネルギーをもらってできたものであるから、電界がない場合にも結晶の中を動きまわっている。しかし、この運動はランダムであり平均すればなくなってしまい熱運動だけで電流が流れることはない。これに電界をかけると、全体としては一方向に移動して電流を流す。
断面積A、長さLの均一な導体があり、電子濃度をｎとする。この導体の両端にVなる電圧をかけ、Iなる電流が流れたとすると
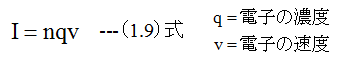
この導体の抵抗が電圧に関係無く一定の場合、すなわちオームの法則が成り立つ場合は、電流Iは電圧Vの比例する。nとqは一定であるから次の関係が成り立つ
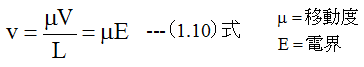
（1.9）式と（1.10）式から
濃度勾配による拡散半導体中のキャリアは熱運動で結晶中を自由に動きまわっている。したがって半導体内部に電界がなく、外界からキャリアが補給されることがなければ、キャリア間の反発力により、拡散現象によりキャリア濃度は一様になるはずである。
いま、何らかの方法で電界のかかっていない半導体の棒の一端からキャリアを連続的に注入すると、はじめは一端にキャリアは集中しているが、拡散現象によりキャリアは濃度の高い方向から低い方に流れる。
単位時間当たりのキャリアの移動数ｊは、濃度勾配dn/dxに比例する。すなわち
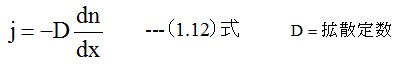
キャリアの移動は電流iが流れることを意味する。キャリアが電子の場合、ｘ方向に流れる電流Iは
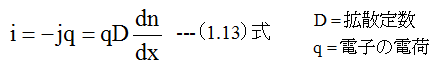
A点から一定の電流を流しこむと、拡散の途中でキャリアが失われることがなければ、定常状態では濃度勾配dn/dx一定となり、ｘ方向に向かって直線的に減少する。
以上はキャリアが電子の場合であるが、ホールにおいても同様な現象が起こる。
移動度μと拡散定数Dの関係式移動度μと拡散定数Dは下記のアンシュシタインの関係で結ばれている。
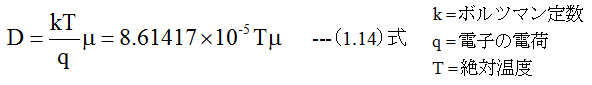
300°Kにおける移動度μと拡散定数Dの値を下記に示します。
| 項目 | 電子移動度 | 電子拡散係数 | ホール移動度 | ホール拡散係数 |
| 記号 | μn | Dn | μｐ | Dp |
| 単位 | cm^2/Vs | cm^2/s | cm^2/Vs | cm^2/s |
| Si | 1200 | 31 | 500 | 13 |
| Ge | 3900 | 101 | 1900 | 49 |
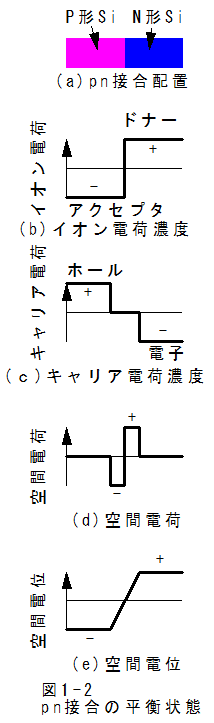
p-n接合GeまたはＳｉの単結晶に右半分はn型、左半分はp型になるように不純物を加えるとその境界にP-n接合を生じる。この場合、p型領域では電子と比較してホール濃度が十分に大きく、ｎ型領域ではその逆になる。
したがって、拡散現象によってホールと電子は互いに他の領域に拡散して一様な濃度になるように見えるが、実際にはキャリアの移動をさまたげる電界ができて一様な濃度とはならない。
図1-2にpn接合の平衡状態、すなわちバイアスがかかっていない場合の状態図をしまします。（ｂ）イオン電荷とは共有結合している原子の電荷であり、アクセプタは電子を補充してマイナスに帯電し、ドナーは電子を放出してプラスに帯電します。原子は共有結合しており移動することはありません。
(c)キャリア電荷とは、ホールと電子による電荷です。ホールと電子は自由に移動できるため、pn接合の境界部で結合し電荷が消滅します。このホールも電子も無い部分を空乏層と呼ぶ。
（ｄ）空間電荷はイオン電荷とキャリア電荷の和であり、pn接合の境界部で発生します。この電荷によりキャリアの移動をさまたげる電界が発生します。
(e)空間電位は空間電荷によって発生します。空間電位の勾配が電界です。
以上はpn接合の平衡状態の定性的説明ですが具体的な計算事例は「特設講座」私の考える半導体物理
１３章：不均一材料に行く。で説明しています。
少数キャリアの拡散不純物半導体では、真性半導体に比べて一方のキャリア濃度は非常に大きく、他方の濃度は非常に小さくなる。この濃度の大きい方のキャリアを多数キャリア、小さいほうを少数キャリアと呼ぶ。したがって、p型半導体ではホールが多数キャリア、n型半導体では電子が多数キャリアとなる。
pn接合に順方向にバイアスを加えた場合、電流がどのように流れるかを考えてみよう。順方向バイアスでホールはp領域からn領域に拡散する。n領域にはいったホールは少数キャリアとなるからこれを小数キャリアの拡散と呼ぶ。（逆に電子はn領域からp領域に拡散する。）
p領域ホールの濃度は
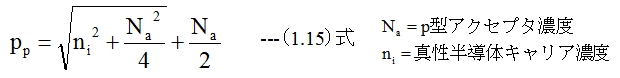
であるが、n領域にはいったホールの濃度は
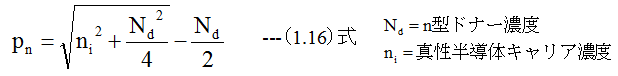
に減少しなければならない。したがって、p領域からn領域に拡散してきたホールは、n領域を多数キャリアの電子と結合して消滅する。
ホールと電子が結合する際、ギャップエネルギー（Siで約1.2eV)に相当する光を発生する。Siの1.2eVは赤外線であり、発光した光を外部に取り出せば発光ダイオードとなる。（通常発生した光は半導体内部で吸収され熱に変わる。）
n領域からp領域に拡散した電子についても全く同様のことがいえる。実際の順方向の電流はホール電流と電子電流の和となる。
次に逆バイアスの場合を考える。n領域のホールの濃度は
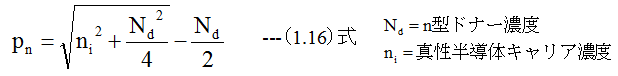
でり、であるが、p領域にはいったホールの濃度は
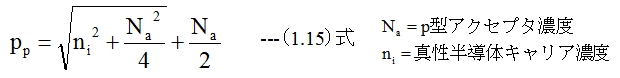
となるが、pn接合部までの電流は少数キャリアとなり電流は小さくなる。電子も同様にpn接合部までの電流は少数キャリアとなり、逆方向電流は小さ くなる。ホールと電子の結合による消滅が無いため、発光しない。
生存時間と拡散長さpn結合において、多数キャリアの領域から少数キャリアの領域に注入されたキャリアは、相手の多数キャリアと結合して減少する。これを再結合と呼ぶ。
再結合の速度は存在する余分な少数キャリアの濃度に比例する。
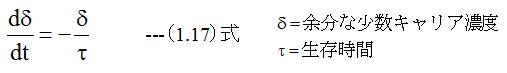
（1.17）式を解くと
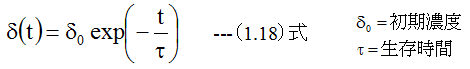
p領域からn領域に注入されたホール濃度をp0とし、これが1/eに減少するまでの距離をLpとするとLpは
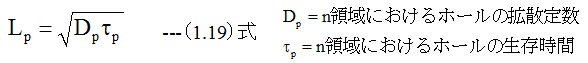
同様にn領域からp領域に注入された電子濃度をｎ0とし、これが1/eに減少するまでの距離をLnとするとLnは
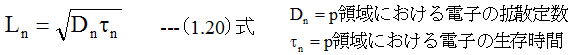
pｎ接合のエネルギーレベル電流は電位（電圧）の高いほうから、電位の低い方向に流れます。しかし、実際の電子の流れは逆方向となります。
ポテンシャルエネルギーは電位×電荷として定義できます。しかし、電子の電荷はマイナスのためポテンシャルエネルギーはマイナスとなってしまいます。
以上の理由により計算式の符号のつけ方に混乱が生じます。どうしたらよいか？一つの案ですが、エネルギーレベルの定義において、プラスの電荷を持つホールを基本的に考えてモデル図を作成します。こうすると符号反転がなく説明がすっきりします。そして電子はホールの逆と考えます。
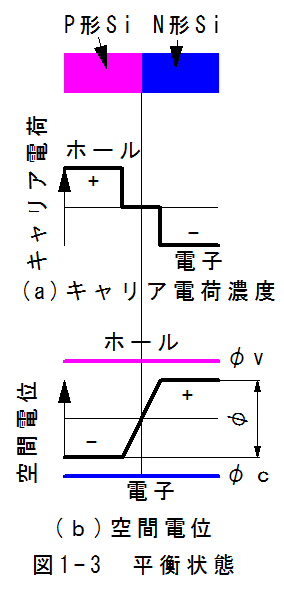
（１）平衡状態
図1-3平衡状態において、(b)空間電位は、ホール電位Φｖを上側に、電子電位Φcを下側に記載しています。これは一般的なエネルギー状態図と逆です。また、電位に電荷をかけるとエネルギーとなり、空間電位と空間エネルギーは同一となります。
pｎ接合のキャリア濃度は、不純物濃度で決定されます。キャリアは一様分布になるような作用が働きますが、キャリアの移動に伴い電位差Φが発生して、キャリアの移動を阻害します。この二つの作用はバランスします。電位差Φを固有障壁電圧と呼ぶ。
キャリアの移動に伴う電位差Φをフェルミレベルは変化しますが、すなおに計算するとｐ型領域でホールは減少し、n型領域で電子が減少することになります。
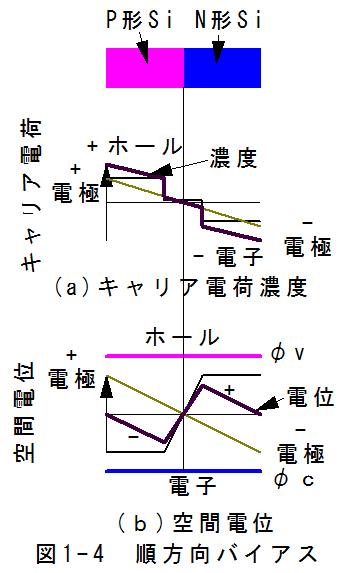（２）順方向バイアスと発光ダイオードの原理図1-4に順方向バイアス時のキャリア電荷濃度と空間電位を示します。p型領域を+電極、n型領域を-電極に接続した場合、p型領域の電位が高くなり、n型領域の電位が低くなります。
キャリア電荷濃度はp型領域のホールが増加し、n型領域の電子が増加します。
電流は電界とキャリア電荷濃度で決定されます。p型領域ではホールは電界、濃度傾斜ともマイナス電極側に作用します。
Pn接合部近傍では逆電界が作用しますが、濃度傾斜が強いためマイナス電極側に作用します。n型領域に到達したホールは電子と結合して消滅します。
電子はホールと逆方向に作用します。
したがって、順方向バイアスでは僅かな電圧で電流が生じ、pn接合近傍でホールと電子の再結合は生じます。このとき、ギャップエネルギー（Siで約1.2eV)に相当する光を発生する。
（３）太陽電池の原理
図1-4は太陽電池の原理図でもあります。pn接合部に光が当たると原子は光のエネルギーを吸収して、ホールと電子を発生します。発生したキャリアは固有障壁電圧Φにより、ホールはｐ型領域に溜まり、電子はn型領域に溜まります。溜まったホールと電子は導線をつなぐと流れだし、電池として作用します。
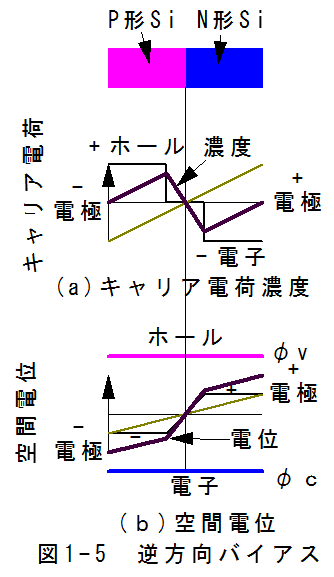
（４）逆方向バイアス時の整流特性とツェナー効果図1-5に逆方向バイアス時のキャリア電荷濃度と空間電位を示します。p型領域を-電極、n型領域を+電極に接続した場合、p型領域の電位が低くなり、n型領域の電位が高くなります。
キャリア電荷濃度はp型領域のホールが減少し、n型領域の電子が減少します。
電流は電界とキャリア電荷濃度で決定されます。p型領域ではホールは電界、濃度傾斜ともマイナス電極側に作用します。電流が流れるためには、pn接合部でホールが生成される必要がありますが、実際には生成されないため、電流はながれません。
電子はホールと逆方向に作用しますが同様に電流は流れません。これがダイオードの整流特性となります。
電圧をギャップエネルギー以上に上げた場合、+電極側にホールが発生します。+電極側で発生したホールは電界により-電極側に流れます。この現象をブレークダウンと呼ぶ。大きな電位差により、+電極側にホール、-電極側に電子ができて逆電流を生じる現象をツェナー効果と呼ぶ。Pn接合近傍の逆電界でキャリアはさらに加速され他の原子と衝突し、さらにキャリアを生成する。これをなだれ増倍作用といい、ガスいり放電管の放電作用と同じである。これは、ツェナーダイオードの原理である。この条件においては、キャリアの再結合は無いため発光はしない。
pn接合のキャリア濃度pｎ接合のエネルギーレベルでは定性的な説明であったが、定量的にはどうなるであろか？
p領域のホール濃度をPp、ｎ領域のホール濃度電子濃度をPn、p領域の電子濃度をNp、n領域の電子濃度をNnとすると
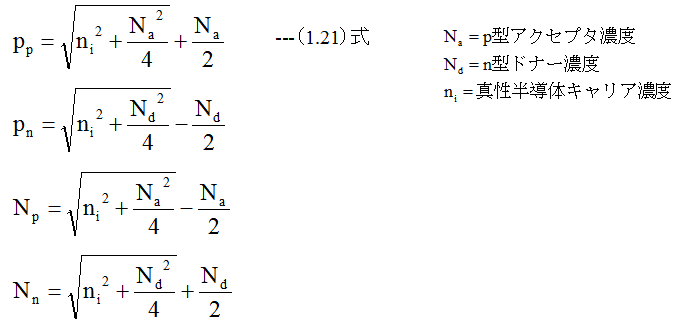
となるはずである。P型半導体とn型半導体を接合するとキャリアの濃度が不均一になるため、キャリアの拡散が生じ空間電荷分布を生じる。これにより電位分布が発生する。（1.21）式から電位分布やキャリア濃度分布を計算するには、電荷密度(σ)と電界(E)の関係式を解く必要があり、大変複雑な計算となる。
条件を限定すれば電荷密度(σ)と電界(E)の関係式を解くことは可能であり、p型領域の電位が小さくなりn型領域の電位が高くなる。また、キャリア濃度は不純物濃度よりも小さくなる。これはキャリアの拡散と電位分布の影響と思われる。
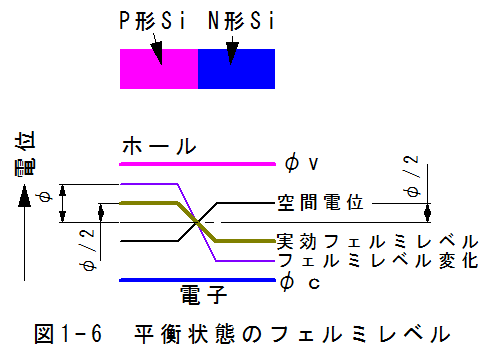
pn接合の整流特性フェルミーディラックの分布関数は真性半導体で定義された関数であり、不純物半導体にフェルミーディラックの分布関数を適用できるか？
厳密には問題がありそうなのですが、不純物半導体にフェルミーディラックの分布関数を適用すると計算式の単純化が可能です。
pn接合で空間電位はp型領域にたいしてｎ型領域の空間電位はΦだけ高くなります。
これをこのように説明します。ｎ型領域に対してp型領域のフェルミレベルは2Φだけ高くなる。このためp型領域のホール濃度が高くなる。pn接合でホールはn型領域に拡散し、ホール濃度は減少するが、空間電位が発生しホールの拡散を防止する。実効的には、ｎ型領域に対してp型領域のフェルミレベルはΦだけ高くなる位置でバランスする。
従って、p領域のホール濃度をPp、ｎ領域のホール濃度電子濃度をPn、p領域の電子濃度をNp、n領域の電子濃度をNnとすると
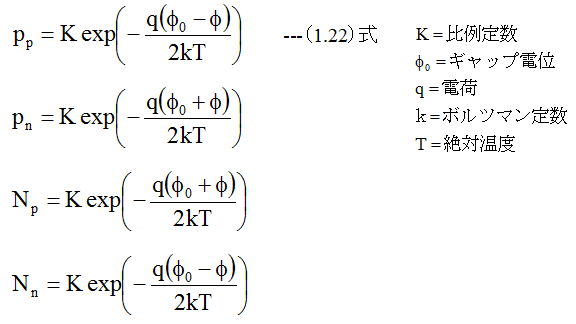
の関係が得られます。今、ｐ型半導体側に電圧Ｖをかけ、n型半導体側をアースに接続した場合
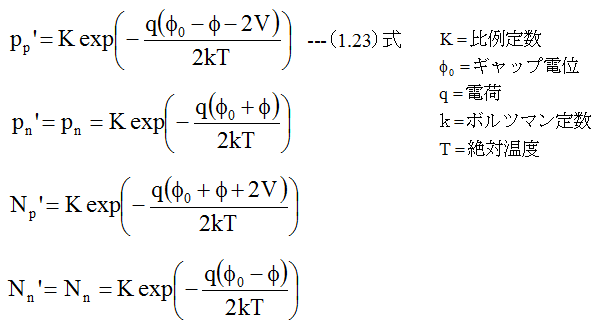
（1.22）式から
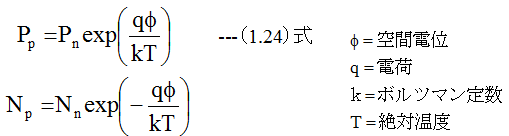
（1.23）式から
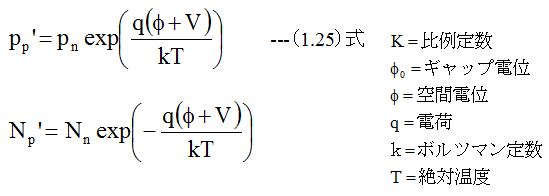
となります。ホールによる電流Ipは
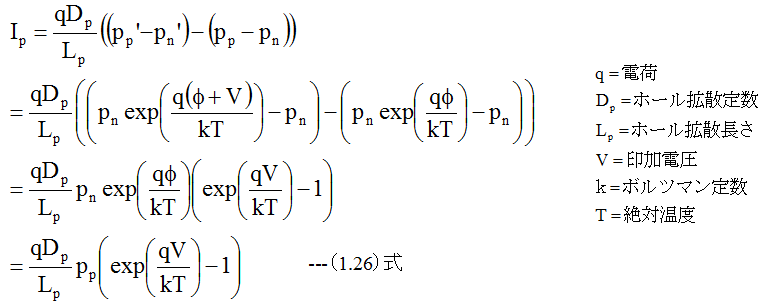
同様に電子による電流Iｎは
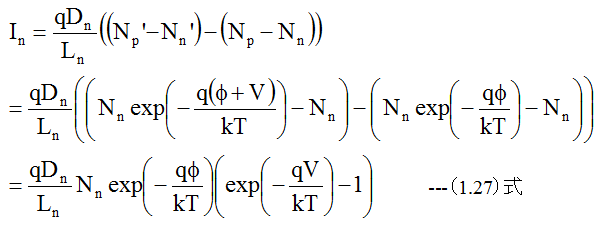
したがって電子の電荷がマイナスを考慮すると全電流Iは
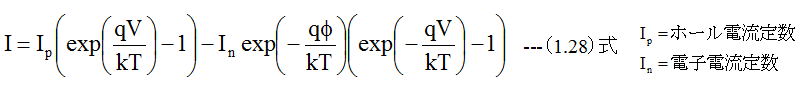
となります。（1.28）式はトランジスタ回路入門記載の理論式
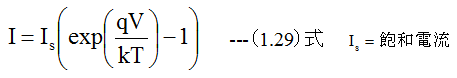
とは一致しません。
（1.28）式においてIp、In、Φは実験的に決定すべき定数であり、それぞれの単位はアンペア(A)、アンペア(A)、ボルト(V)の単位を持つ。
qは電子電荷であり1.6E-19(C)、kはボルツマン定数であり1.38E-23(J/deg)、Tは絶対温度300°K、Vは印加電圧(V)、Iは電流(A)ある。
（1.28）式と（1.29）式の比較この２つの式の違いを検討してみよう。
まず、（1.29）式で我々が自由に決定できる定数は[Is]のみである。[Is]は逆方向印加時の飽和電流を意味している。仮に定数[Is]を下記のように決定する。
[Is]=1 (μA)
次に（1.28）)式においては、定数Ip、InとΦの値を決定しなければならない。
(16-12)式と(16-14)式の比較から定数Aは
[Ip]=[In]=1 (μA)
Φはn型半導体とp型半導体の電位差であり、逆方向印加時の耐圧を表わしている。定数Φは
Φ=0.5 (V)
以上の条件での（1.28）式と（1.29）式の計算結果のグラフを図1-7に示す。
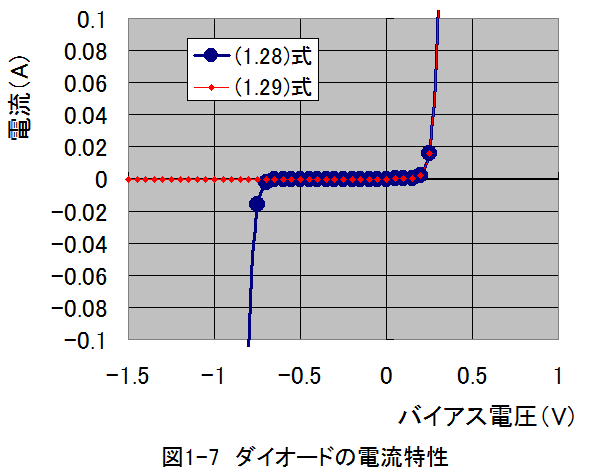
図1-7から明らかなように逆方向印加時の耐圧0.5(V)以上で(1.27)式と(1.28)式は良く一致している。しかし、逆方向印加時の耐圧0.5(V)以下の領域では(1.27)式は急激に電流が増加するのに対し、(1.28)式は変化しない。
経験的ではあるが、逆方向印加時の耐圧以下の領域で急激に電流が増加する現象を確認しており、これをブレイクダウンまたはツェナー現象と呼んでいる。従って、(1.27)式の方がより実際の特性を近似しているといえる。また、(1.27)式によれば、逆方向印加時の耐圧はｎ型とp型のポテンシャル差によりもので不純物濃度差を大きくすれば、逆方向印加時の耐圧が大きくなることを示している。
また、(1.27)式誘導の前提条件として、n型半導体側をアースに接続、p型半導体側をバイアスとした。この条件において、プラスバイアスはホールが電流の主体となり、マイナスバイアスで電子が電流の主体となります。
p型半導体側をアース、n型半導体側をバイアスとした場合、この逆となります。すなわち、アースの接続条件により、ダイオードの電流理論式の形が変化します。
一般に電位は電界の積分として求めることができますが、この場合、電位は相対値が重要で絶対値はあまり問題となりません。しかし、半導体のキャリア濃度を与える式は電位の絶対値が重要となります。
どうも、自然界はプラスとマイナスの電荷がうまくバランスしているようです。すなわち、プラスとマイナスの電荷がバランスした点が電位ゼロとなります。
そして、容量の大きい物質ほど電位ゼロとなりやすい。すなわち地球電位に接続することをアースと呼びます。
pn接合の静電容量pn接合は空乏層をはさんでp領域とn領域が向かいあっているのでこの部分に静電容量を持つ。空乏層の幅は印加電圧によって変化し、順方向バイアスの場合は狭くなり、逆方向バイアスの場合は広くなるので、容量も変化する。
pn接合の変化が急峻の場合の静電容量Cは
pn接合の変化が緩やかな場合の静電容量Cは
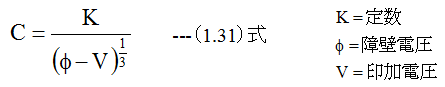
このために作られたダイオードをバリキャップダイオードといい、自動周波数制御回路に実用化されている。
ダイオードの応用ダイオードの応用としては
（１）整流用（一般向け）
（２）定電圧制御用（ツェナーダイオード）
（３）自動周波数制御用（バリキャップダイオード）
（４）照明用（発光ダイオード）
（５）DVD用（半導体レーザ）
（６）発電用（太陽電池）
等があるが、動作原理的にはほぼ同じと考えることができます。個々の特性の改善検討は、多くの場合実験的に検討されます。
おそらく、全ての条件を理論的に導くことは困難なため、個々のダイオードについてはそのダイオーの評価データを参照する必要があります。