RLC測定回路図4-1にRLC測定回路を示します。
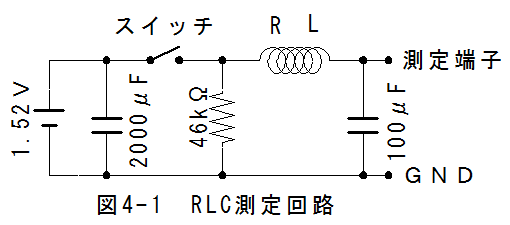
スイッチがOFFのとき、測定端子とGNDは46kΩの抵抗を通して短絡されます。また、乾電池の内部抵抗の影響を無くすため、十分大きな容量のコンデンサを乾電池と並列にいれました。測定用にはコイルと直列に115μFのコンデンサを使用しました。また、コイルはインダクタンスLと直流抵抗Rがあるとします。 スイッチをONするとコイルLとコンデンサCに電源電圧1.52Vが印加されます。
RLC回路の基礎理論抵抗RとコイルLとコンデンサCの電圧を加算すると電源電圧V0に等しくなります。したがって
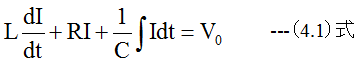
（4.1）式を電荷ｑに置き換えると
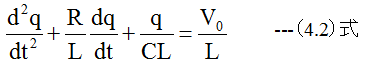
（4.2）式は2階線形微分方程式であり、ラプラス変換法で代数解を求めることができます。初期条件でｑ＝0、q'=0としてラプラス変換すると
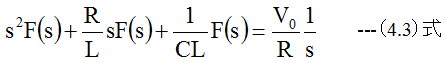
（3.3）式を変形すると
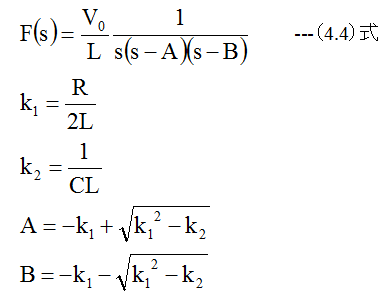
となります。したがって、（4.4）式をラプラス逆変換すると
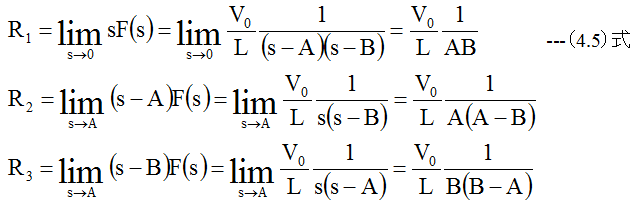
したがって（4.2）式の解は
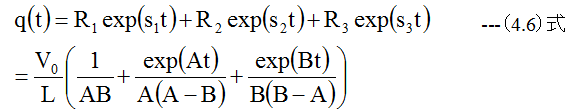
となります。しかし、（4.6）式はわかりにくいので整理する必要があります。振動が起こる条件は
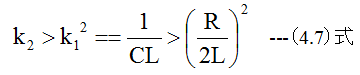
です。この条件において
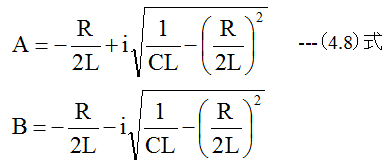
です。さらに展開するならば
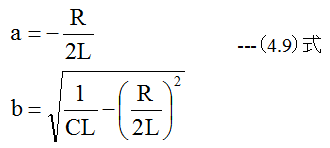
として、（4.6）式は以下のように変形できます。
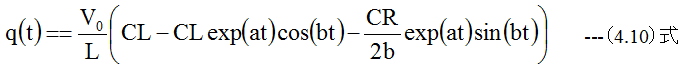
コンデンサ間の電圧は
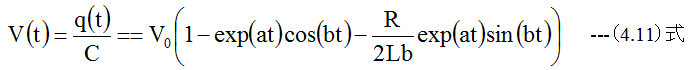
となります。式の展開の過程が複雑ですので、得られた結果が正しいか？検証が必要なようです。
連立ルンゲクッター法による計算（１）計算式
連立ルンゲクッター法を適用すると比較的簡単に計算できます。
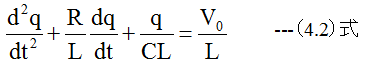
（4.2）式を以下のように変形します。
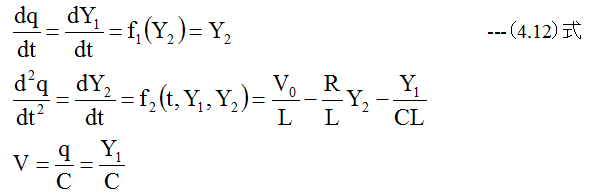
（4.12）式は一見難解ですが、（4.2）式から簡単に変形できます。（4.12）式の条件を設定して連立ルンゲクッター法を適用すると数値計算による解が求まります。
具体的な計算は「微分方程式RCL回路.xls」を使用します。
（２）「微分方程式RCL回路.xls」のダウンロード
「微分方程式RCL回路.xls」は以下からダウンロードできます。
[ 微分方程式RCL回路.xls]をダウンロードする。ダウンロード後は、ダブルクリックで保存場所を指定して保存してください。
評価結果（１）計算条件
・抵抗R=4Ω
・コンデンサ容量C=100μF
・インダクタンスL=0.0042H
・時間間隔dt=0.2ms
（２）評価結果グラフ
評価結果グラフを図4-2に示します。
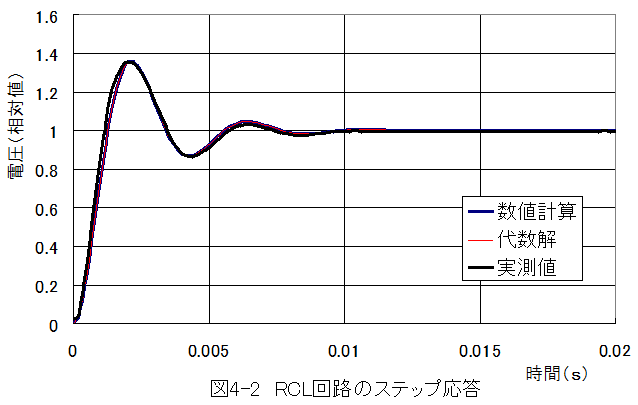
結果の検討（１）ラプラス変換法で求めた代数解と連立ルンゲクッター法による数値計算結果はほぼ完全に一致する。
（２）ラプラス変換法の式の展開は複雑で解が求まるのは限られるが、計算精度が良く、計算時間が短い。
（３）連立ルンゲクッター法による数値計算は式の変形が容易であるが、計算時間が長くなる。また、計算条件によっては計算誤差が大きくなる。
（４）実測値は代数解（および数値計算結果）とだいたいにおいて、類似した波形形状となる。（厳密には一致していない。）
（５）コイルの直流抵抗は1Ω以下であるのに対して、実測値と類似の減衰係数を求めると約4Ωとなる。
（６）ステップ応答の減衰係数が大きくなる理由としては、振動電流による電磁波の放出が考えられる。
（７）一般的なコイルはインダクタンスLが小さく、簡易オシロでの測定に適さない。
（８）大まかなインダクタンスLは代数解（および数値計算結果）と実測値を比較することにより、求めることができます。
（９）ステップ応答は、不安定で正確な測定が難しい。インダクタンスLの正確な測定は、別な方法を考える必要がありそうです。
５章：CR回路交流特性に行く。