キットで遊ぼう電子回路 No.1基本編vol.1簡単な電気実験を行うには、電子部品の準備が必要となります。個別に電子部品を準備するのは面倒なので、キットで遊ぼう電子回路 No.1基本編vol.1を購入しました。
（１）発売元
・株式会社アドウィン
http://www.adwin.com/index.html
キットで遊ぼう電子回路No.1
基本編vol.1
型番：ECB-100T
価格：￥3,570 （税込）
（２）アマゾン amazon.co.jp
アドウィンからの直接購入も可能ですが、アマゾンからも購入できます。
基本編Vol.1セット [キットで遊ぼう電子回路シリーズ1] [ムック]
価格： ￥ 3,570 通常配送無料
（３）付属の電子部品リスト
| 部品名 | 備考 | 型番 | 数量 |
| ブレッドボード | - | MB-102 | 1 |
| 線材 | ブレッドボード配線用 | - | 一式 |
| 抵抗 | 220Ωカーボン抵抗 | 1/4W | 2 |
| 抵抗 | 820Ωカーボン抵抗 | 1/4W | 3 |
| 抵抗 | 2.2ｋΩカーボン抵抗 | 1/4W | 3 |
| 抵抗 | 15ｋΩカーボン抵抗 | 1/4W | 1 |
| 可変抵抗 | 100ｋΩVR | B100ｋΩ | 1 |
| LED | 赤 | - | 4 |
| LED | 黄 | - | 3 |
| LED | 緑 | - | 3 |
| ダイオード | - | 1S1588 | 3 |
| 電解コンデンサ | 33μF | - | 3 |
| プッシュスイッチ | - | - | 3 |
| トグルスイッチ | 単極双投 | HTS-103 | 1 |
| 電池ボックス | 単３×４（６V）用 | - | 1 |
ブレットボードを使用すると、はんだごてを使用しないで、回路を構成でき、大変便利です。抵抗、LED、ダイオード、コンデンサ等は不要となった家電製品から回収可能ですが、新品の電子部品は使いやすいです。
LED特性評価回路LED特性評価回路を図6-1に示します。Ch1とCh2の電圧を測定してLEDに加わる電圧と流れる電流を測定します。
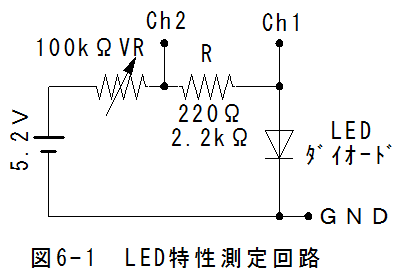
評価条件
LED 赤 R=220Ω
LED 黄 R=220Ω
LED 緑 R=220Ω
ダイオード 1S1588 R=2.2kΩ
評価結果（１）順方向電流特性
順方向電流特性を図6-2に示します。
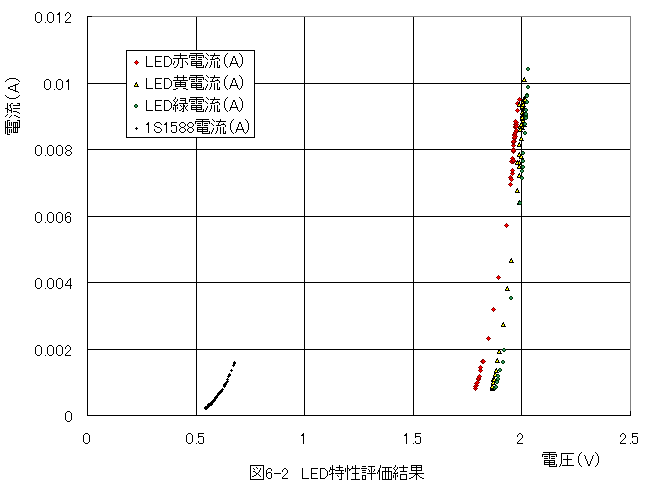
評価データ詳細は下記ファイルを参照願います。
LED特性評価結果「6-1.xls」に行く。（２）逆方向電流特性
逆方向に流れる電流は、全てのLEDとダイオードにおいて、測定限界以下（ゼロ）でした。
ダイオードの電流特性理論式（１）ダイオードの電流特性理論式
トランジスタ回路入門記載の理論式
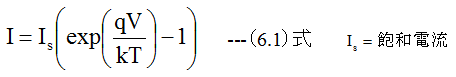
半導体物理から導いた理論式は
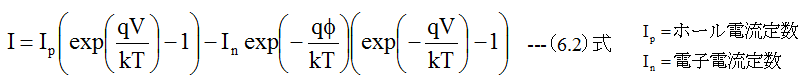
となります。上記の2個の式は、逆バイアスのブレイクダウンまたはツェナー領域を除き良く一致します。上記の式で測定結果の電流特性を近似できるのでは？
そう思って、いろいろとパラメータを変えて近似を試してみました。
（２）ダイオードの電流特性理論式よる近似の結果
結論として、「ダイオードの電流特性理論式で実測した電流特性を近似できない！！」という結果となりました。
（３） ダイオードの電流特性理論式の問題点
ダイオードの電流特性理論式は式の誘導の過程で、電流による過熱が考慮されていません。半導体自身の抵抗をゼロとして式を誘導しています。
実際には、電流により熱が発生し、半導体が過熱され、原子が激しく振動することにより、電子と原子の衝突が起こり、抵抗値が上昇すると思われます。
一定以上の電流で、PN接合の破壊温度に達することが、予想されます。ダイオードの電流特性理論式は発熱の影響を考慮していないため、破壊電流の予測もできません。
破壊温度に達する限界電流は、実験的に求めるきりないはずです。（限界電流を求める実験は電子部品の破壊を伴います。）
LED電流特性の4次多項式近似LED電流特性は4次多項式で精度良く近似できます。近似結果を以下に示します。
| 型式 | 4次係数 | 3次係数 | 2次係数 | 1次係数 | 0次係数 | 相関R2 |
| LED赤 | -2.9639 | 22.361 | -63.101 | 78.974 | -37.003 | 0.9975 |
| LED黄 | -35.069 | 270.54 | -782.23 | 1004.7 | -483.68 | 0.985 |
| LED緑 | 0.6806 | -5.3286 | 15.937 | -21.496 | 10.99 | 0.9989 |
| 1S1588 | -0.5303 | 1.2895 | -1.1276 | 0.4275 | -0.0598 | 0.9974 |
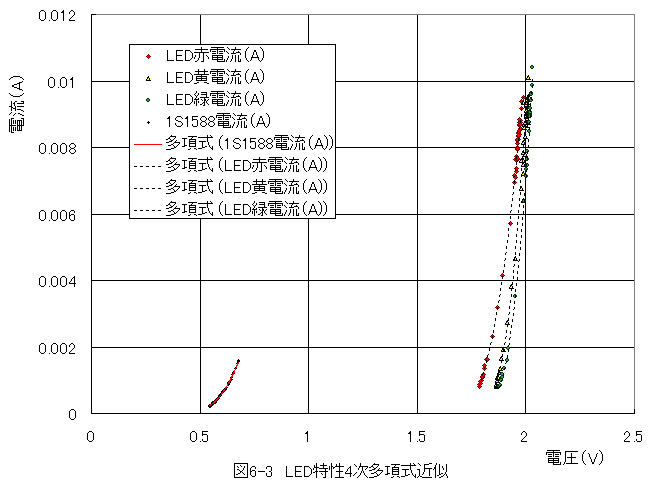
LED電流特性の直線近似LED電流特性は4次多項式で精度良く近似できますが、数学的に扱いにくくなります。若干の近似誤差を無視して直線近似すると扱いやすくなります。
| 型式 | 1次係数 | 0次係数 | 相関R2 |
| LED赤 | 0.0433 | -0.0769 | 0.9881 |
| LED黄 | 0.061 | -0.1133 | 0.9774 |
| LED緑 | 0.0618 | -0.1161 | 0.9837 |
| 1S1588 | 0.009 | -0.0047 | 0.9636 |
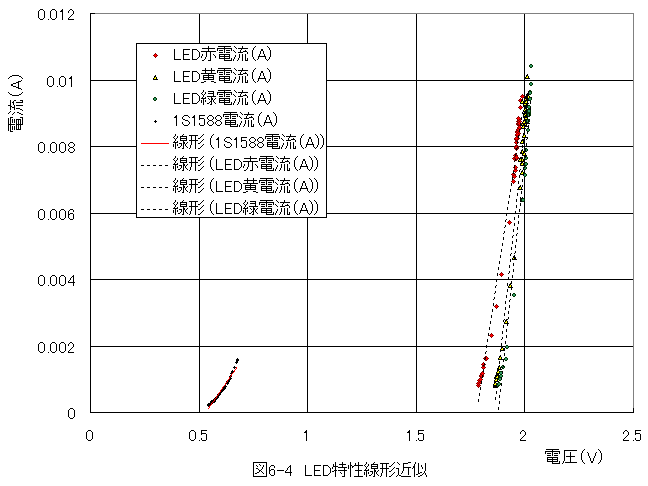
線形近似式を変形して
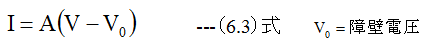
とするならば
| 型式 | A(1/Ω） | V0（V) |
| LED赤 | 0.0433 | 1.77598 |
| LED黄 | 0.061 | 1.857377 |
| LED緑 | 0.0618 | 1.87864 |
| 1S1588 | 0.009 | 0.5222 |
とするならば
| 型式 | R（Ω） | V0（V) |
| LED赤 | 23.094688 | 1.775981524 |
| LED黄 | 16.3934426 | 1.857377049 |
| LED緑 | 16.18122977 | 1.878640777 |
| 1S1588 | 111.111111 | 0.52222222 |
障壁電圧V0と発光波長量子論によるならば、光のエネルギーと波長の関係は下記の式で表わされます。
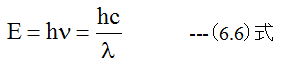
（6.6）式において、ｈはプランク定数、νは光の振動数、ｃは光速、λは光の波長です。
光のエネルギーの単位はeVで示します。これをグラフにすると図6-5に示すようになります。
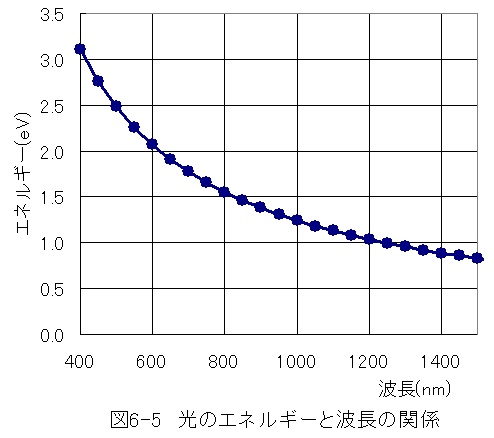
図6-5からわかるように緑（波長550nm）のエネルギーは約2.2eVとなります。これに対して、LED緑の障壁電圧V0は約1.88Vです。
本来ならば、緑（波長550nm）の光を発光するには、2.2V以上の電圧が必要なのでは？
光のエネルギー以下の電圧で発光する理由としては、電流によるPN接合部の過熱の影響がかんがえられます。1.88Vの電位差で加速された電子は、PN接合部の原子の熱運動からエネルギーを得て、2.2eVのエネルギーに達した電気振動を起こし、電気振動に応じた電磁波を放出すると考えられます。
また、このエネルギーが大きいほど、発光波長は短くなることになります。実験結果も正確ではありませんが、障壁電圧が高い方が、波長が短くなることを示しています。
LEDは受光素子として使用できるか？発光素子と受光素子の基本構造は同じです。したがって、LEDは受光素子として動作するはずです。
確認のため、LED赤を2個向かい合わせて設置し、片側に電流を流して発光させ、もう一方のLED に流れる電流を測定してみました。
実験結果を図6-6に示します。
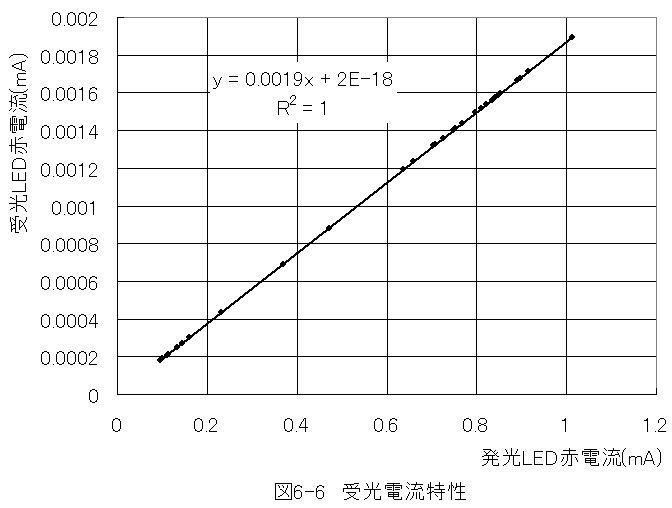
図6-6は横軸が発光LED赤の電流、縦軸が受光LED赤の電流です。直線近似の相関R2=1という驚くべく結果です。
ただ、効率は約2％と悪く流れる電流は微小です。
結果の検討（１）電気・電子工学を専門としないエンジニアにおいても、一般物理として電気の特性を学習します。抵抗、コンデンサ、コイルの特性は数学的にすっきりしており、理解しやすいのですがダイオードやトランジスタは難解です。
（２）ダイオード電流特性の理論式を導くには、難解な半導体物理を理解する必要があります。
（３）今回のLED特性評価でわかったこと！！難解な理論を展開して導いたダイオード電流特性の理論式が実際のLEDの電流特性に適用できないということがわかりました。
（４）ダイオード電流特性の理論式と実測値の比較は、多くの時間をかけて検討してみました。しかし、どうしても一致しないというのが結論です。
（５）机上理論がうまく適用できない場合、多くの実験や経験が重要となります。
（６）電子工学は、多くの実験や経験が重要な分野のようです。