業務用としては、microsoft officeを使用するのが一般的ですが、趣味用としては少し高価です。 OpenOfficeはフリーで使えますがmicrosoft officeと完全互換ではありません。
これまでに作成したEXCEL(.xls）ファイルからOpenOffice(.ods）ファイルへの変更を検討します。
EXCEL(.xls）ファイルのダウンロード（１）トップページから「EXCELで学ぶ複素関数のページに行く。」をクリックします。
（２）「３章：高次方程式のフリープログラムに行く。」をクリックします。
（３）「ワークブック「「6次方程式.xls」」をダウンロードする。」をクリックします。
（４）警告「f21-2.exeはダウンロードしたユーザ数が少ないため、PCに問題を起こす可能性があります。」が表示されます。
（５）「実行」ボタンをおします。
（６）警告「WindowsによってPCが保護されました」が出ます。
（７）「詳細情報」をクリックします。
（８）「実行」ボタンが表示されるので、 「実行」ボタンを押します。
（９）自己解凍ダイアログが表示されます。
（１０）「OK」ボタンを押します。
（１１）ファイル「複素関数1.xls」が保存されます。
ファイル名の変更（１） OpenOfficeを起動します。
（２）「ファイル」＿「開く」を選択します。
（３）「 6次方程式.xls 」を開きます。
（４）メニューの「ファイル」＿「名前を付けて保存」を選択します。
（５）保存場所はデスクトップ、ファイル名を「 OpenOfficeCalc_9.ods」とします。
（６）ファイルの種類は「ODF表計算ドキュメント(.ods)」とします。
（７） 「保存」ボタンを押します。
（８）ここでいったんOpenOfficeＣａｌｃを終了します。
（９）デスクトップに「 OpenOfficeCalc_9.ods 」ファイルがあります。
ファイル「OpenOfficeCalc_9.ods」の変更（１）ファイル「OpenOfficeCalc_9.ods」をダブルクリックで起動します。
（２）メニューの「ツール」＿「マクロ」＿「マクロの管理」＿「OpenOffice Basic」を選択します。
（３）OpenOffice Basic マクロダイアログで「 OpenOfficeのマクロ」＿「 OpenOfficeCalc_9.ods 」を選択します。
（４）「新規作成」ボタンを押します。
（５）新しいモジュールダイアログで名前を「Module1」のまま「OK」ボタンを押します。
（６） OpenOfficeBasicのIEDウインドウが開きます。
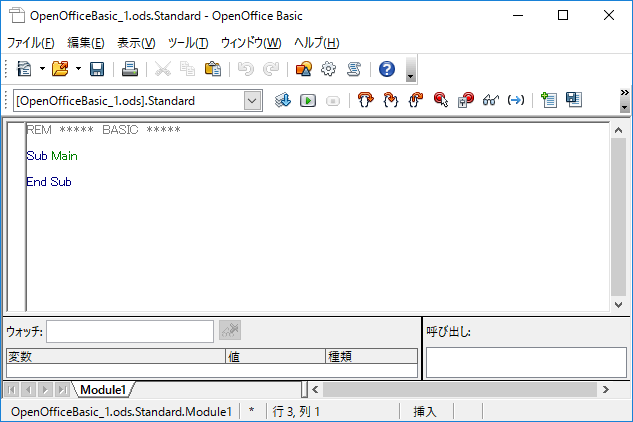
（７） 以下のプログラムコードを書き込みます。
Sub Main
sh1 =ThisComponent.getSheets.getByName ("Sheet1")
'初期入力
N=sh1.getCellByPosition( 2,4).Value
dR=sh1.getCellByPosition( 2,5).Value
dS=sh1.getCellByPosition( 2,6).Value
R=sh1.getCellByPosition( 2,7).Value
S=sh1.getCellByPosition( 2,8).Value
'初期出力
sh1.getCellByPosition( 0,36).Value=0
sh1.getCellByPosition( 1,36).Value=R
sh1.getCellByPosition( 2,36).Value=S
'繰り返し演算
For i = 1 To N Step 1
f0=sh1.getCellByPosition( 2,32).Value
g0=sh1.getCellByPosition( 2,33).Value
sh1.getCellByPosition( 2,7).Value=R - dR
frm=sh1.getCellByPosition( 2,32).Value
grm=sh1.getCellByPosition( 2,33).Value
sh1.getCellByPosition( 2,7).Value=R + dR
frp=sh1.getCellByPosition( 2,32).Value
grp=sh1.getCellByPosition( 2,33).Value
sh1.getCellByPosition( 2,7).Value=R
sh1.getCellByPosition( 2,8).Value=S-dS
fsm=sh1.getCellByPosition( 2,32).Value
gsm=sh1.getCellByPosition( 2,33).Value
sh1.getCellByPosition( 2,8).Value=S+dS
fsp=sh1.getCellByPosition( 2,32).Value
gsp=sh1.getCellByPosition( 2,33).Value
'偏微分値の算出
fr = (frp - frm) / (2 * dR)
gr = (grp - grm) / (2 * dR)
fs = (fsp - fsm) / (2 * dS)
gs = (gsp - gsm) / (2 * dS)
'次のRとS(Θ）値を算出
R = R - (f0 * gs - g0 * fs) / (fr * gs - fs * gr)
S = S - (fr * g0 - f0 * gr) / (fr * gs - fs * gr)
'次のRとS(Θ）値を設定
sh1.getCellByPosition( 2,7).Value=R
sh1.getCellByPosition( 2,8).Value=S
'次のRとS(Θ）値を出力
sh1.getCellByPosition( 0,36+i).Value=i
sh1.getCellByPosition( 1,36+i).Value=R
sh1.getCellByPosition( 2,36+i).Value=S
Next i
End Sub
（８）メニューの「表示」＿「ツールバー」＿「フォームコントロール」を選択します。
（９）フォームコントロールダイアログの「デザインモードオン／オフ」ボタンでオン状態にします。
（１０）ボタン上でマウスを右クリックし、「コントロール」を選択します。
（１１）「属性 プッシュボタン」の「イベント」タブの「実行時」の右端のボタンをクリックします。
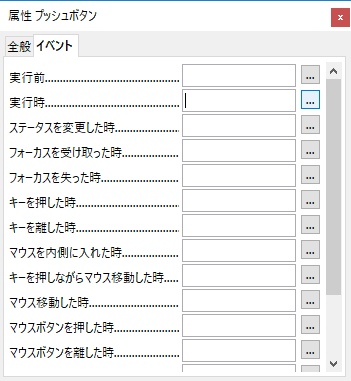
（１２）現われた「アクションの割り当て」の「実行時」を選択し、「マクロ」ボタンを押します。
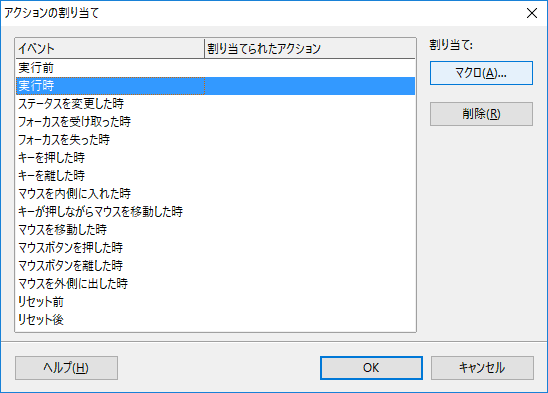
（１３）「マクロセレクター」の「OpenOfficeCalc_9.ods」＿「Standard」＿「Module1」＿「Main」 を選択して「OK」ボタンを押します。
（１４） 「アクションの割り当て」の「OK」ボタンを押します。
（１５） 「属性 プッシュボタン」を閉じます。
（１６）フォームコントロールダイアログの「デザインモードオン／オフ」ボタンでオフ状態にします。
（オフ状態でないと動作しません！！）
（１７）フォームコントロールダイアログを閉じます。
（１８）「計算実行」ボタンを押します。
（１９）R=1→1.12425994614029、Θ＝1→0.927441814446686に変化します。
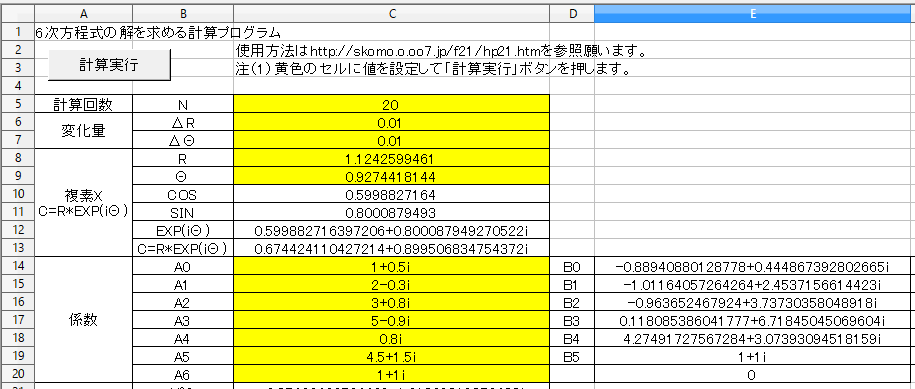
（２０）上記の結果は６次方程式
A6*X^6+ A5*X^5+ A4*X^4+ A3*X^3+ A2*X^2+ A1*X+A0=0 が
(X-C)*(B5*X^5+ B4*X^4+ B3*X^3+ B2*X^2+ B1*X+B0)=0
に変換出来たことを意味します。
すなわち６次方程式は１つの複素数の解と５次方程式に変換できます。
（２１）同様に５次方程式は１つの複素数の解と4次方程式に変換できます。
（２２）最終的には以下６個の複素数解を得ることができます。
| C1 | 0.674424110427214+0.899506834754372i |
| C2 | -0.0784236791913897-0.596907248451527i |
| C3 | -0.125439481517976+0.612333790442077i |
| C4 | -0.52671166229616-0.244666810796106i |
| C5 | 0.261135596325401-0.850009597794161i |
| C6 | -3.20498488374709+1.67974303184535i |
（２３）メニュー「ファイル」＿「保存」を選択します。
OpenOfficeCalc_9.odsのダウンロードOpenOfficeCalc_9.odsは以下からダウンロードできます。
OpenOfficeCalc_9.odsをダウンロードする。９章EXCEL→OpenOfficeファイル変換のまとめ（１） 「EXCELで学ぶ複素関数」の 「f21-2.exe」は、自己解凍型のファイルにしたため、ダウンロードではかなりの警告がでます。（昔は自己解凍型のファイルが扱いやすく便利と思ったのですが、現在は危険ファイル扱いになるようです。）
（２） 「EXCELで学ぶ複素関数」の「6次方程式.xls」はマクロの全面書き直しとなりました。
（３）マクロは互換性がありません。
（４）EXCELの標準設定では、複素関数機能がOFFに設定されています。複素関数機能を使うには、メニューの「ツール(T)」＿「アドイン(I)」を選択し、アドインリストの「分析ツール」にチェックマークを設定する必要があります。
（５）OpenOfficeCalcでは、標準設定で複素関数機能が有効で互換性がありました。
（６）マクロの全面書き直しはさほど難しい作業ではありませんでした。
（７）何のために高次方程式の解を求める必要があるのか？ラプラス逆変換以外の用途はあまりないとおもいます。
（８）ラプラス逆変換は微分方程式の代数解を求めるのに重要ですが、とにかく難しい！！
（９）実用的には、微分方程式の解はルンゲクッタ法を使用したほうが簡単です。
１０章：「EXCELで学ぶ複素関数」「5章」のファイル変更に行く。