矩形信号の発生矩形信号発生条件は１章と同一となります。
矩形信号波形データの保存矩形信号波形データの保存は、１章と同一となります。
整流回路図2-1に整流回路図を示します。
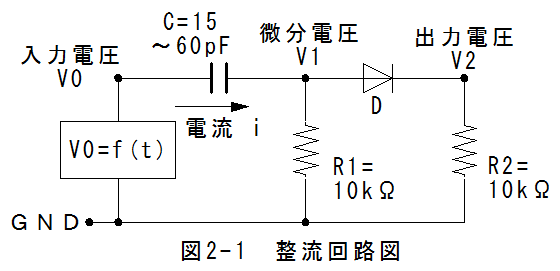
図2-1において、入力電圧はArduino(アルドゥイーノ) unoを使用し、 矩形信号の発生スケッチ1（プログラム1）を使用します。
矩形信号波形データはHantek 6022BE PC USB 2CH デジタルオシロスコープを 使用して保存したデータを使用します。
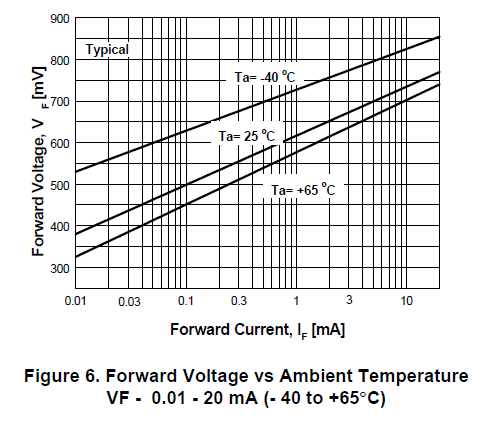
ダイオードの電圧・電流特性記号Dはダイオードであり、仮に1N4148とするならば、電流・電圧特性は以下のようになります。
ダイオードの電圧・電流特性を定数AとBを用いて、下記の式で近似します。
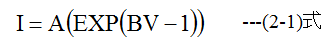
Ta=25℃のグラフから1mAで620ｍV、0.01mAで325ｍVとするならば
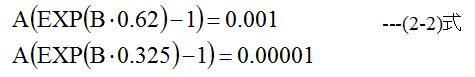
（2.2）式はゴールシークを使って解くことができます。定数AとBを代入すると
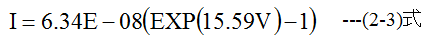
となります。ダイオード1N4148電圧・電流特性をグラフ化すると以下のようになります。
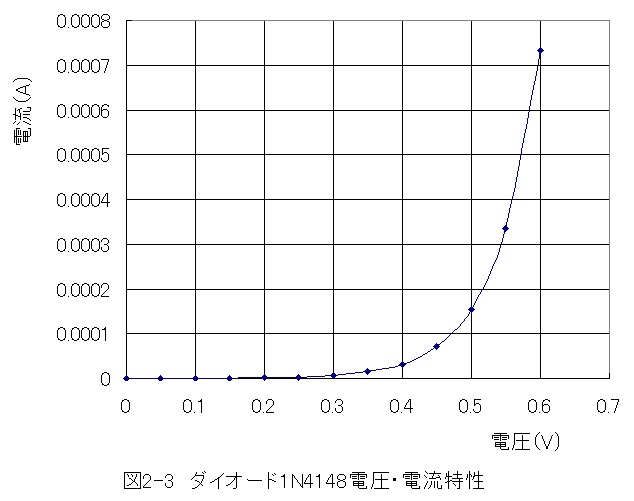
ダイオードの電圧・電流特性図2-1からダイオードの両端の電圧Vは
また出力電圧V2は
です。電流Iは以下の条件式から求めます。
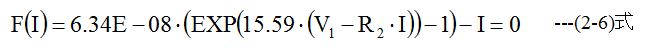
（2.6）式を満足する電流Iはニュートン法を用いて求めることができます。電流Iの初期値は
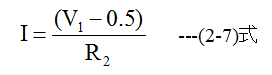
とします。補正1回目の電流は
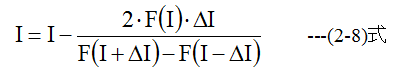
で計算します。 (2-8)式の計算を繰り返すと精度が高くなりますが、とりあえず5回とします。
2-1.xls（整流回路の計算）のダウンロード2-1.xls（整流回路)の計算）は以下からダウンロードできます。
2-1.xls（整流回路の計算）をダウンロードする。2-1.xlsはOpenOffice 4.1.3でも問題無く動作しました。
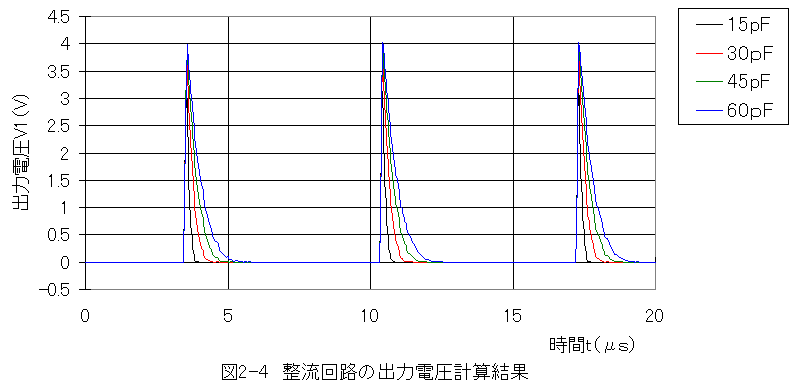
コンデンサ容量15〜60pFでの計算結果グラフコンデンサ容量15〜60pFでの計算結果グラフを以下に示します。
周波数＝145kHz
時間間隔Δｔ=0.0625μs
抵抗R1=R2=10kΩ
コンデンサ容量15〜60pFでの実測結果グラフコンデンサ容量15〜60pFでの実測結果グラフを以下に示します。
周波数＝145kHz
時間間隔Δｔ=0.0625μs
抵抗R1=R2=10kΩ
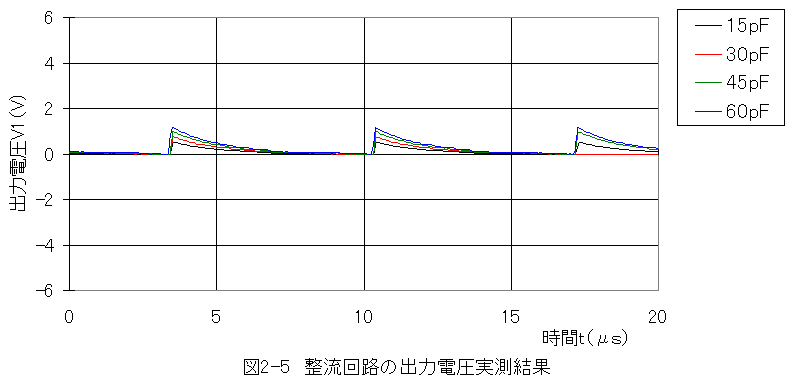
整流回路の簡易計算方法の検討まとめ（１）整流回路の出力電圧波形の検討において、計算結果と実測結果が大幅に異なる結果となりました。
（２）計算では近似計算誤差が発生します。
（３）実測では、鋭い波形にオシロスコープが追従できない可能性があります。
（４）真値を知るのは難しいのですが、今回はオシロスコープの波形追従性誤差が大きいように思えます。
（５）計算はマクロを使用しないため扱いが容易です。
3章：積分回路の簡易計算方法の検討に行く。