矩形信号の発生矩形信号発生条件は１章と同一となります。
矩形信号波形データの保存矩形信号波形データの保存は、１章と同一となります。
積分回路図3-1に積分回路図を示します。
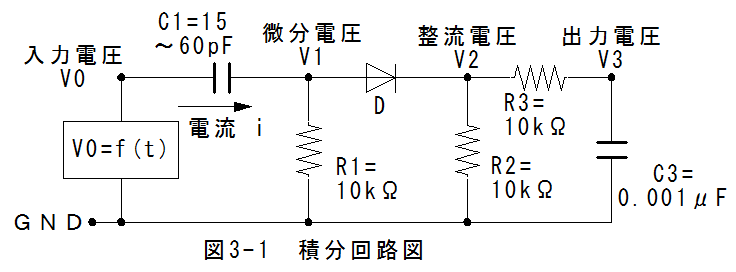
図3-1において、入力電圧はArduino(アルドゥイーノ) unoを使用し、 矩形信号の発生スケッチ1（プログラム1）を使用します。
矩形信号波形データはHantek 6022BE PC USB 2CH デジタルオシロスコープを 使用して保存したデータを使用します。
このデータを「V0=f(t)」とします。
コンデンサーに蓄積される電荷Q（単位クーロン）は電流をi（単位A)とすると
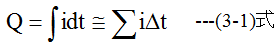
抵抗とコンデンサの電圧の和は、入力電圧に等しくなります。すなわち
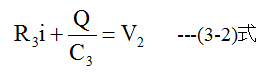
出力電圧V1は
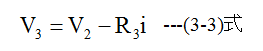
電荷Qの初期値をゼロとするならば、 (3-2)式から電流iが求まります。
電流iが決定されれば、 (3-1)式から電荷Qの計算ができます。
電流iが決定されれば、 (3-3)式から出力電圧V3が計算できます。
これらの計算はEXCELの表計算で実行できます。
3-1.xls（積分回路の計算）のダウンロード3-1.xls（積分回路)の計算）は以下からダウンロードできます。
3-1.xls（積分回路の計算）をダウンロードする。3-3.xlsはOpenOffice 4.1.3でも問題無く動作しました。
コンデンサ容量15〜60pFでの計算結果グラフコンデンサ容量C1=15〜60pF（C3=0.001μF）での計算結果グラフを以下に示します。
周波数＝145kHz
時間間隔Δｔ=0.0625μs
抵抗R1=R2=R3=10kΩ
容量C1=15〜60pF（C3=0.001μF）
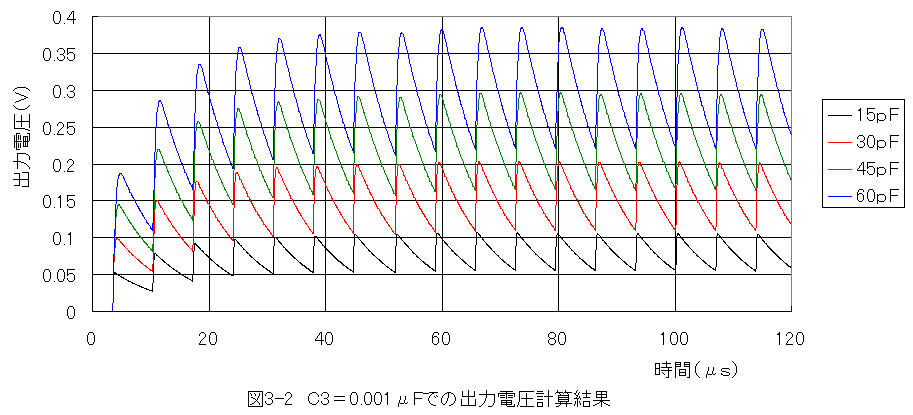
コンデンサ容量C1=15〜60pF（C3=0.001μF）での実測結果グラフコンデンサ容量C1=15〜60pF（C3=0.001μF）での実測結果グラフを以下に示します。
周波数＝145kHz
時間間隔Δｔ=0.0625μs
抵抗R1=R2=R3=10kΩ
容量C1=15〜60pF（C3=0.001μF）
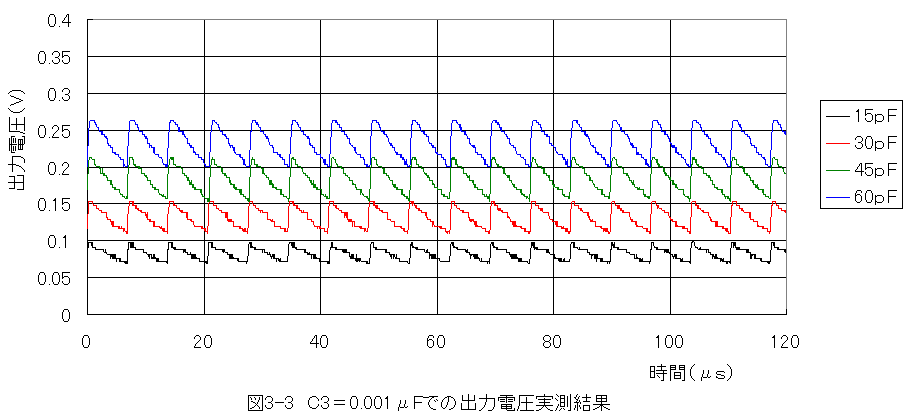
コンデンサ容量C1=15〜60pF（C3=1μF）での実測結果グラフコンデンサ容量C1=15〜60pF（C3=1μF）での実測結果グラフを以下に示します。
周波数＝145kHz
時間間隔Δｔ=0.0625μs
抵抗R1=R2=R3=10kΩ
容量C1=15〜60pF（C3=1μF）
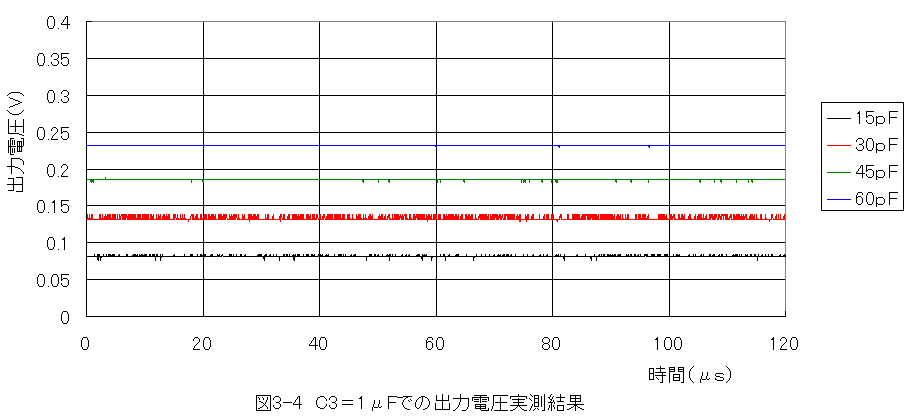
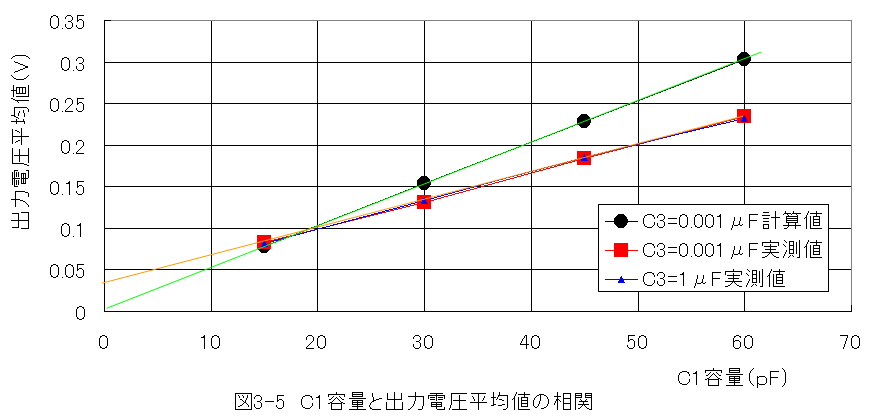
C1容量と出力電圧平均値の相関グラフ図3-2と図3-3の出力電圧は変動が大きいので平均値を求める必要があります。
C1容量と出力電圧平均値の相関グラフを以下に示します。
周波数＝145kHz
時間間隔Δｔ=0.0625μs
抵抗R1=R2=R3=10kΩ
容量C1=15〜60pF
積分回路の簡易計算方法の検討まとめ（１）積分回路の出力電圧波形の検討において、計算結果と実測結果は波形がにてきましたが、 変動電圧に差があります。
（２） C1容量と出力電圧平均値の相関において、計算値は原点を通る直線の関係がえられました。
（３）実測では、直線の関係がありますが、オフセットがあります。
（４）オフセット誤差の要因としては、配線容量の影響等が考えられます。
（５）計算も実測もC1容量と出力電圧平均値の相関において直線関係があり、本条件で15〜60ｐF程度 の容量測定が可能であることが確認できました。
（６）計算はマクロを使用しないため扱いが容易です。
4章：矩形波→正弦波変換回路の簡易計算方法の検討に行く。