矩形信号の発生矩形信号発生器として、Arduino(アルドゥイーノ) unoを使用します。
詳細は
Arduino(アルドゥイーノ) unoを参照願います。矩形信号の発生スケッチ（プログラム）
//tone
void setup()
{
tone(13, 23300);
}
void loop()
{
}
解説：（１）13番ピンに周波数23300Hzの矩形信号を出力します。
（２）設定可能な最大周波数は65535Hzです。
（３）設定可能な最小周波数は31Hzです。
矩形信号波形データの保存矩形信号波形データの保存は、Hantek 6022BE PC USB 2CH デジタルオシロスコープを使用します。
詳細は
Hantek 6022BEデジタルオシロスコープとAMラジオを参照願います。補足説明
（１）Windows7からWindows10にアップグレード後正常動作しなくなりました。
（２）Hantek 6022BEデジタルオシロスコープを接続後、「システム」＿「デバイスマネージャー」＿「Hantek622BE DRIVER 2」 を更新する必要がありました。
（３）Time/divの設定と保存時の時間間隔Δｔには以下の関係がありました。
| No | Time/div | Δｔ |
| 1 | 500us | 1us |
| 2 | 200us | 1us |
| 3 | 100us | 1us |
| 4 | 50us | 1us |
| 5 | 20us | 0.25us |
| 6 | 10us | 0.125us |
| 7 | 5us | 0.0625us |
| 8 | 2us | 0.02us |
| 9 | 1us | 0.01us |
>矩形波→正弦波変換回路図4-1に>矩形波→正弦波変換回路を示します。
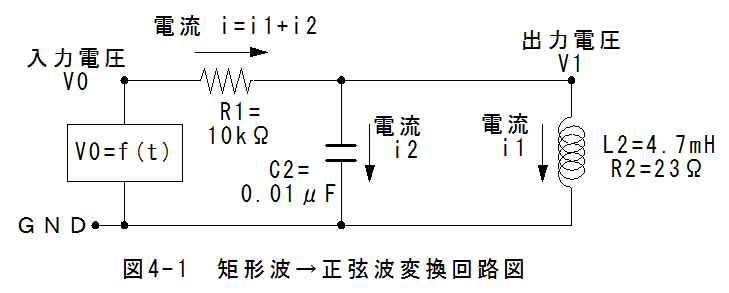
図4-1において、入力電圧はArduino(アルドゥイーノ) unoを使用し、 矩形信号の発生スケッチ1（プログラム1）を使用します。
矩形信号波形データはHantek 6022BE PC USB 2CH デジタルオシロスコープを 使用して保存したデータを使用します。
このデータを「V0=f(t)」とします。
電流i1の関係式は
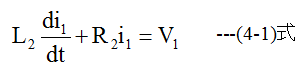
電流i2の関係式はQを電荷とすると
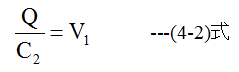
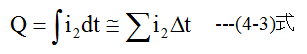
出力電圧V1は
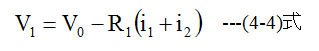
電荷Qの初期値をゼロとするならば、 (4-2)式からV1=0となります。
電流i1初期値をゼロとするならば、 (4-4)式からi2が求まります。
i2から電荷Qの値が更新されます。そしてV1の値も更新されます。
(4-1)式から(di1)/(dt)の計算ができます。
(di1)/(dt)からi1の値が更新されます。
これらの計算はEXCELの表計算で実行できます。
4-1.xls（矩形波→正弦波変換回路の計算）のダウンロード4-1.xls（矩形波→正弦波変換回路の計算）は以下からダウンロードできます。
4-1.xls（矩形波→正弦波変換回路の計算）をダウンロードする。4-1.xlsはOpenOffice 4.1.3でも問題無く動作しました。
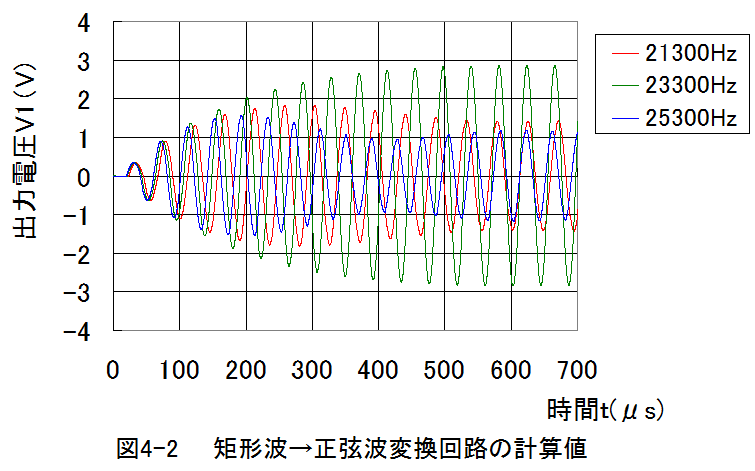
周波数21300Hz〜25300Hzでの計算結果グラフ周波数21300Hz〜25300Hzでの計算結果グラフを以下に示します。
周波数＝21300Hz〜25300Hz
時間間隔Δｔ=0.25μs
抵抗R1=10kΩ
容量C2=0.01μF
インダクタL2=4.7mH(内部抵抗23Ω)
周波数21300Hz〜25300Hzでの実測結果グラフ周波数21300Hz〜25300Hzでの実測結果グラフを以下に示します。
周波数＝21300Hz〜25300Hz
時間間隔Δｔ=0.25μs
抵抗R1=10kΩ
容量C2=0.01μF
インダクタL2=4.7mH(内部抵抗23Ω)
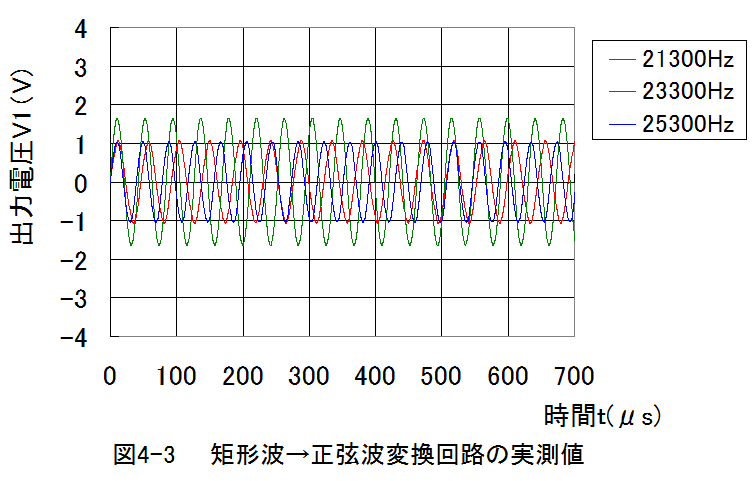
矩形波→正弦波変換回路の簡易計算方法の検討まとめ（１）矩形波→正弦波変換回路の出力電圧波形の検討において、計算結果と実測結果共に矩形波→正弦波変換 できることが確認できました。
（２）計算結果と実測結果共に共振周波数23215Hzに近い周波数で最大振幅となることが確認できました。
（３）最大振幅の大きさは計算結果より実測結果の方が小さくなりました。
（４）内部抵抗R2=23Ω→ R2=70Ωにすると最大振幅の大きさが計算結果と実測結果で一致します。
（５）計算はマクロを使用しないため扱いが容易です。