屈折の法則
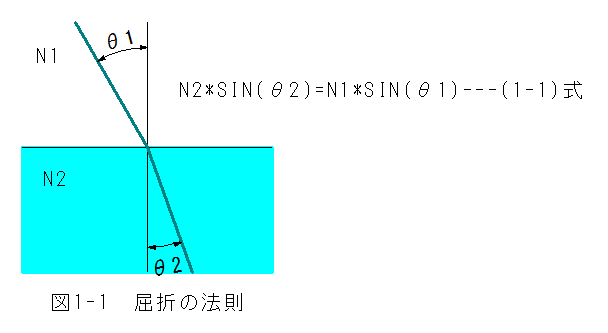
図1-1 屈折の法則において、N1は入射側の屈折率、θ1は入射側の法線に対する角度、N2は出射側 の屈折率、θ2は出射側の法線に対する角度です。
ここで、以下の関係式が成立します
。 N2*SIN(θ2)=N1*SIN(θ1)---(1-1)式
(1-1)式は2次元と3次元光線追跡で成立する基本的な関係式です。
平凸レンズ焦点距離
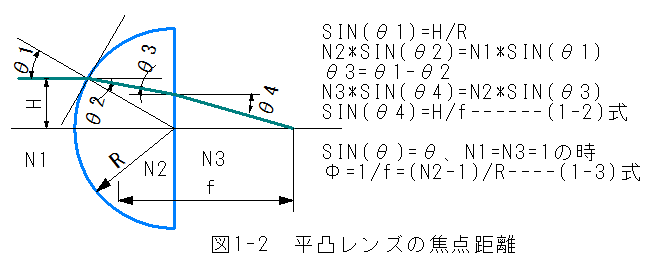
図1-2 平凸レンズ焦点距離においてHは平行光線の像高、Rはレンズの曲率半径、θ1はレンズ法線に対する角度です。ここで以下の関係式が成立します。
SIN(θ1)=H/R
入射側の屈折率をN1、レンズ法線に対する出射角度をθ2、出射側の屈折率をN2としたとき
N2*SIN(θ2)=N1*SIN(θ1)
平面の法線に対する入射角度θ3は
θ3=θ1-θ2
入射側の屈折率をN2、法線に対する出射角度をθ4、出射側の屈折率をN3としたとき
N3*SIN(θ4)=N2*SIN(θ3)
焦点距離をfとしたとき
SIN(θ4)=H/f------(1-2)式
となります。 (1-2)式は順番に計算することにより、値を求めることができますが、焦点距離fは、像高Hの値により変化します。
近軸理論の簡易計算式
近軸理論では角度θが十分小さいとき
SIN(θ)=TAN(θ)＝ θ
と近似して計算式を簡略化します。SIN(θ)=θ、N1=N3=1でレンズパワーをΦとしたとき
Φ=1/f=(N2-1)/R----(1-3)式
と簡易計算式を得ることができます。近軸理論の簡易計算式は光軸近傍のみに適用できる近似解ですので、実際の光学系では大きな誤差を生じます。
2次元光線追跡レンズの特性を詳しく知るには、光線追跡計算が不可欠となります。光線追跡計算を行うにあたっては、必ずしも計算原理式を完全に理解する必要はありません。
光線追跡計算プログラムの使用方法を理解すれば、光線追跡計算を行うことができます。しかし計算の原理を理解すりことも重要です。
光線追跡計算プログラムの使用方法は2次元も3次元もにていますが、計算の原理は2次元の方が容易に理解できます。
2次元光線追跡計算式の原理
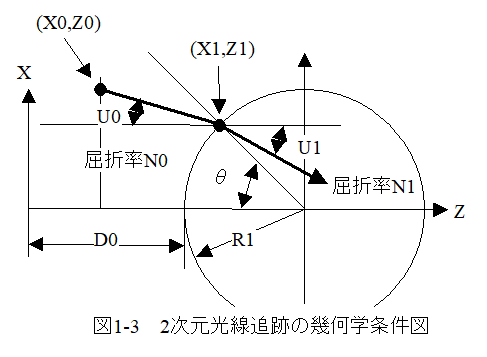
図1-3の2次元光線追跡の幾何学条件図から2次元光線追跡計算式を導きます。
（１）入力パラメータ
入力パラメータは下記のとおりとなります。
Z0：入射光光軸方向座標
X0：入射光像高X方向座標
U0：入射光のX方向角度
R1：レンズ面の曲率半径
D0：レンズ面の光軸方向距離
Ox1：レンズX方向オフセット
N0：入射側の屈折率
N1：出射側の屈折率
（２）中間パラメータ
入力パラメータから計算される中間パラメータ下記のとおりとなります。
θ：レンズ面法線の角度
（３）出力パラメータ
最終的に計算される出力パラメータは下記のとおりとなります。
Z1：出射光光軸方向座標
X1：出射光像高X方向座標
U1：出射光のX方向角度
（４）関係式
入射光の直線の方程式から
X1=X0 - (tan(U0))*(Z1 - Z0) -------(1-4)式
レンズ面の円の方程式から
(X1-Ox1)^2 +(Z1- D0 -R1)^2 = R1^2 -------(1-5)式
屈折の法則から
N0*SIN(θ - U0) = N1*SIN(θ - U1) -------(1-6)式
幾何学条件図から
TAN(θ）= (X1-Ox1)/(D0+R1 - Z1) -------(1-7)式
以上の関係式が成立します。
未知数が中間パラメータ(θ)、出力パラメータ(Z1,X1,U1)の4個に対して、関係式が4個成立します。
従って、(1-4)(1-5)(1-6)(1-7)式の関係から出力パラメータ(Z1,X1,U1)を求めることができます。
なお本計算式はXZの2次元絶対座標系を用いています。従って、レンズ間隔は相対的な間隔ではなく絶対座標で入力する必要があります。しかし、絶対座標系ゆえにオフセット等が面毎に独立に変更でき混乱が少なくなるメリットがあります。
2次元光線追跡の実際の計算式(1-4)(1-5)(1-6)(1-7)式は計算するには適さない形をしているため、計算しやすいように変形する必要があります。
変形後の計算式は下記の通りとなります。
XB= X0+tan(U0)*Z0-Ox1
A=1+(tan(U0))^2
B=-2*(D0+R1+tan(U0)*XB
C=D0^2 +2*D0*R1+ XB^2
凸面の場合(R>0の場合)
Z1=(-B-sqrt(B^2 -4*A*C))/(2*A)
凹面の場合(R<0の場合)
Z1=(-B+sqrt(B^2 -4*A*C))/(2*A)
X1=X0-tan(U0)*(Z1-Z0)
θ=ATAN((X1-Ox1)/(D0+R1-Z1))
U1= θ-ASIN(N0*sin(θ-U0)/N1)
入力パラメータをZ[i],X [i],U [i] 等の配列データで定義すれば、出力パラメータはZ[i+1],X [i+1],U [i+1] となり、次々と計算を進めることが可能です。
実際の計算プログラムVBAでの実際の計算プログラムをSub CAL()に示します。サブルーチン内変数（i,XB,A,B,C,R,SX)以外の変数はあらかじめDim N(60), Rr(60), D(60), X(60) ,U(60), Z(60), Ox(60), NUMBと定義しておきます。
(1)NUMBにはレンズ面数を設定します。
(2) Rr(i)にはレンズ曲率半径の逆数を設定します。（平面の場合はRr(i)=0とします。）
(3) N(i), D(i), ,Ox(i)の値を設定します。（ D(i)の値は絶対座標で入力します。）
(4) X(0) ,U(0), Z(0)の初期値を設定します。
(5)以上の設定完了後にSub CAL()を呼び出すとNUMB - 1までのX(i) ,U(i), Z(i)の値が計算されています。
Sub CAL()
For i = 0 To NUMB - 2
If (Rr(i + 1) = 0) Then
Z(i + 1) = D(i)
X(i + 1) = X(i) - Tan(U(i)) * (Z(i + 1) - Z(i))
SX = 0
U(i + 1) = SX - Application.WorksheetFunction.Asin(N(i) * Sin(SX - U(i)) / N(i + 1))
Else
R = 1 / Rr(i + 1)
XB = X(i) + Tan(U(i)) * Z(i) - Ox(i + 1)
A = 1 + Tan(U(i)) ^ 2
B = -2 * (D(i) + R + Tan(U(i)) * XB)
C = D(i) ^ 2 + 2 * D(i) * R + XB ^ 2
If R > 0 Then
Z(i + 1) = (-B - Sqr(B ^ 2 - 4 * A * C)) / (2 * A)
Else
Z(i + 1) = (-B + Sqr(B ^ 2 - 4 * A * C)) / (2 * A)
End If
X(i + 1) = X(i) - Tan(U(i)) * (Z(i + 1) - Z(i))
SX = Atn((X(i + 1) - Ox(i + 1)) / (D(i) + R - Z(i + 1)))
U(i + 1) = SX - Application.WorksheetFunction.Asin(N(i) * Sin(SX - U(i)) / N(i + 1))
End If
Next i
End Sub
光路長と波面収差
レンズ性能の評価は波面収差で判断します。理想的なレンズでは、焦点面での光路長さが等しくなる必要があります。全ての光線が焦点面で一点に収束し、各光線の光路長さが等しいとき、波面収差は0となり理想レンズの特性を示します。
理想レンズとは、光線の波面が焦点面で一点に収束する完全な球面波となるレンズです。しかし実際のレンズでは完全な球面波とはならずゆがんだ波面となります。波面収差とは完全な球面波からの光路誤差を定量的に表現した誤差量で通常、光路誤差を波長で割った値を用います。
(1)パターン面から結像面までの総光路長の計算
波面収差を計算するにはまず最初にパターン面から結像面までの総光路長(OLa)を計算します。光路長さは光線追跡で光線位置X(i)、Z (i)と角度U (i)および屈折率N (i)から実際の光路長さに屈折率をかけた値の総和として求めます。総光路長(OLs)は下記式で計算します。
OLa=Σ(Z(i+1) - Z(i)) * N(i) / Cos(U(i)) ------------(1-8)式
(i=0からi=N-1まで計算、 N-1は結像面）
(2)総光路長を焦点面の一点からみた光路長(OLb)に補正
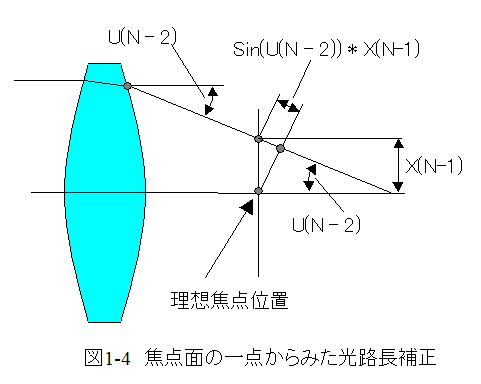
図1-4に示すように(1-8)式の結果を焦点面の一点からみた光路長(OLb)に補正する計算は下記式となります。
OLb= OLa+Sin(U(N - 2)) * X(N-1) ------------(1-9)式
（ U(N - 2)は結像面の一つ前の面の光線角度、 X(N-1)は結像面の光線高さ）
収差の一般的な表示単位としてはλが用いられます。波長λとすると
波面収差(OL)=光路長さ誤差(OLb)/ λ ------------(1-10)式
となります。
2章：光学ガラスの選定に行く。