１３章：不均一材料
１２章までは均一な半導体材料の特性について論じてきた。しかし、不純物の濃度が一様でない半導体材料を考えると面白いことがおこる。
しかし、３次元的に不純物の濃度が一様でない半導体材料での自由電子や正孔の挙動はかなり、難解な理論となる。ここでは、議論を単純化するため、１次元的にドナ、アクセプタ濃度勾配のある、長い棒の半導体を考えてみる。
静電ポテンシャルΦ(x)とキャリア（自由電子と正孔）の関係
図13-1に示す不純物の濃度が一様でない半導体材料においては、「７章：不純物濃度と[po][no]積」自由電子となるエネルギー(Ec)が (7-5)式、荷電子帯のエネルギー(Ev)が(7-6)式で与えられる。
また、静電ポテンシャルΦ(x)はエネルギーを電荷qで割ったものであり、自由電子となる静電ポテンシャルΦc(x)が (7-7)式、荷電子帯の静電ポテンシャルΦv(x)が(7-8)式で与えられる。
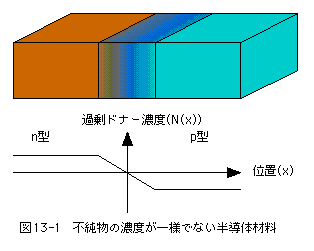
図13-1に示す不純物の濃度が一様でない半導体材料においては、過剰ドナー濃度N(x)はxの関数として変化する。従って、静電ポテンシャルΦ(x)はxの関数として変化する。しかし、過剰ドナー濃度N(x)と静電ポテンシャルΦ(x)の関係式はかなり難解なものとなる。
まず、過剰ドナー濃度N(x)と静電ポテンシャルΦ(x)の関係式を求める前に、準備運動が必要である。最初に、自由電子の密度[no](x)、正孔の密度[po](x)と静電ポテンシャルΦ(x)との関係式を求めよう。
我々はすでに「４章：ボルツマン分布」(4-12)式でエネルギーと自由電子の密度[no](x)、正孔の密度[po](x)の関係が成立することを学んでいる。
静電ポテンシャルΦ(x)と自由電子の密度[no](x)、正孔の密度[po](x)の関係において下記関係式が成立する。
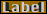- 電荷密度(σ)と電界(E)の関係式
いよいよ、難解な式が出てくる。電荷密度(σ)、電界(E)、誘電率(ε)とすると下記の関係式が成立する。
div(εE)=σ ------(13-3)
(13-3)式の意味するのは何であろうか？
まず、静電気の基本に戻ってみよう。距離rだけ離れた電荷qと電荷q'に働く反力Fは（13-4）式となる。
F=qq'/(4πεr^2) ---(13-4)
電荷qから距離rだけ離れた点の電界(E)は
E=q/(4πεr^2) ---(13-5)
誘電率(ε)と電界(E)の積εEは
εE=q/(4πr^2) ---(13-6)
となる。(4πr^2)は球の面積であり、(13-6)は単位面積あたりの電荷量を意味する。
さて、(13-3)式にはdiv（発散という）という見なれない記号がある。これは何を意味するのであろうか？ さて、(13-3)式にはdiv（発散という）という見なれない記号がある。これは何を意味するのであろうか？
電界(E)のx,y,z成分をそれぞれEx,Ey,Ezとした場合、(13-3)式は(13-7)式に書き直される。
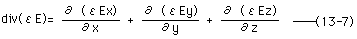
ますます、わからない？(13-7)式は何を意味するのだ。このいみを理解するため、「図13-2 単位体積に流入する流量Qと流出する流量Q+ΔQ」を考えてみよう。
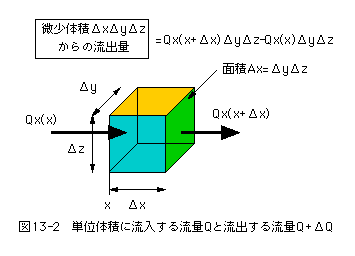
「図13-2 単位体積に流入する流量Qと流出する流量Q+ΔQ」において
Qx(x+Δx)-Qx(x)=(∂Qx/∂x)Δxの関係がある。従って
微少体積ΔxΔyΔzからの流出量=(∂Qx/∂x)ΔxΔyΔz ----(13-8)
となる。(13-8)式はx方向の流出量のみであるがy,z方向も同様に求め加算する必要がある。ただし、y,z方向の流出が零の場合は省略できる。
(13-3)および（13-7）式は(13-8)式を微少体積ΔxΔyΔzで割ったものであり、単位体積あたりの流出量を意味している。
- 電界(E)とポテンシャル（電位）Φとの関係式
電界(E)とポテンシャル（電位）Φの間には下記の関係式が成立する。
E=-∇Φ ----(13-9)
(13-9)には、またまた意味不明の記号∇（ナブラと読む）が出てきた。(13-9)式を書き直すと電界(E)のx,y,z成分をそれぞれEx,Ey,Ezとすると
Ex=-∂Φ/∂x ----（13-10）
Ey=-∂Φ/∂y ----（13-11）
Ez=-∂Φ/∂z ----（13-12）
となる。ちなみにx方向の電界(Ex)は次のようにも書ける。
Ex=-(Φ(x+Δx,y,z)-Φ(x,y,z))/Δx ----（13-13）
実際の計算は（13-13）式で行う。(13-9)式は複雑な計算式をスマートに表現しただけである。
- 過剰ドナー密度Nと電荷密度σの関係式
「７章：不純物濃度と[po][no]積」(7-2)式で論じたように電荷密度σ＝0の場合は自由電子の数を[no]､正孔の数を[po]とすると下記関係式が成立する。
[no] - [po]= N ----(13-14)
電荷密度σ≠0で正の電荷の数を[Np]とすると
[Np]=N+[po]-[no] ----(13-15)
従って、キャリアの電荷量をqとすると電荷密度σは、
σ=q(N+[po]-[no]) ----(13-16)
となる。
- 過剰ドナー密度Nとポテンシャル（電位）Φの関係式
(13-3)式に(13-9)式と(13-16)式を代入すると
div(-ε∇Φ)=q(N+[po]-[no]) ----(13-17)
さらに、(13-17)式に(13-1)(13-2)式を代入すると
div(-ε∇Φ)=q(N+[ni]Exp(-qΦ/kT)-[ni]Exp(qΦ/kT)) ----(13-18)
となり、変数は過剰ドナー密度Nとポテンシャル（電位）Φの関係式となる。
(13-18)式は大変複雑な式であり、図13-1に示したように過剰ドナー密度Nはx方向のみの関数とし、y、z方向の電界を0とするならば、(13-18)式は下記のように単純化できる。
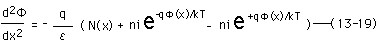
(13-19)式は過剰ドナー密度N(x)が任意の関数として定義されており、一般的に代数的に解を求めることは難しい。
- 数値計算「ルンゲ・クッタ法」
一般的な微分方程式の解を求める方法は、我々は既に「「特設講座」有能エンジニアのための実用数値計算」「３章：常微分方程式」で学んでいる。数値計算「ルンゲ・クッタ法」を適用すればよい。計算はやや面倒であるが、やもえないのである。
さて、数値計算「ルンゲ・クッタ法」を適用するにしても、(13-19)式だけでは、計算条件が不足している。
まずは、過剰ドナー密度N(x)を図13-3に示すように定義する。
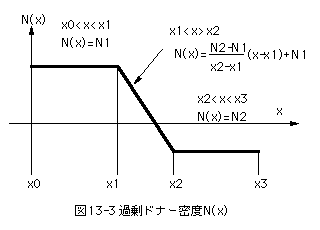
(13-19)式を解くためには、初期条件ΦとdΦ/dxを決定しなければならない。過剰ドナー密度N(x)を図13-3に従うとすれば、x=0(=x0)においてはdΦ/dx=0となる。次にポテンシャルΦの初期値であるが、ポテンシャル（電位）は相対的なものであり、絶対値そのものも意味はあまりない。
従って、x=0(=x0)においてはΦ=0として問題はない。しかし、(13-1)(13-2)式の関係式を満足するためには過剰ドナー密度N=0の時、Φ=0にしなければならない。
これについては、とりあえずx=0(=x0)においてはΦ=0で計算し、N=0となる
x=-(x2-x1)N1/(N2-N1)+x1 ----(13-20)
でのΦの値を[Φo]とし、補正後のポテンシャルΦ'を下記式で求めれば良い。
Φ'=Φ-[Φo] ----(13-21)
１４章：数値計算「ルンゲ・クッタ法」の実行に行く。
- トップページに戻る。