１７章：ダイオードのその他特性

　「１６章：ダイオードの整流特性」では大胆に単純化したモデルを用いて、ダイオードの整流特性を表わす(16-14)式を導きだすことができた。この式はダイオードのツェナー現象をうまく表現できており、大変有効な式と思われる。
　しかし、ダイオードの詳細特性を十分に理解するには、「１３章：不均一材料」の(13-3)式に戻る必要がある。(13-3)式は3次元の式であり、これを1次元にした(13-19)式は数値計算「ルンゲ・クッタ法」で解くことができる。
　「１４章：数値計算「ルンゲ・クッタ法」の実行」では特定の条件で計算を行い、「１５章：計算結果の検討」ではこの計算結果をグラフ化した。

　しかし、(13-19)式を満足する解は一通りではなく、無限にあることを忘れてはならない。ここでは、電界初期値を0→2E+5(V/m)および0→-2E+5(V/m)した場合の変化について検討したい。
  1. 　ポテンシャル電位Φ(V)の電界初期値の影響

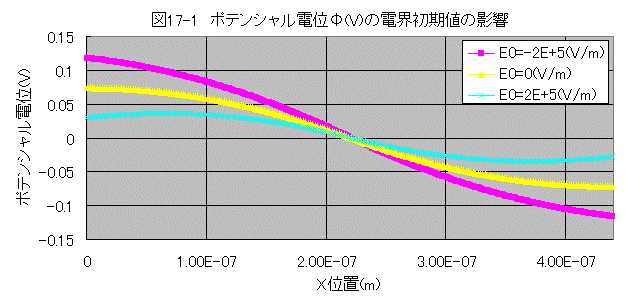
    　図17-1において、E0=2E+5(V/m)は逆方向の印加電圧を意味し、逆方向の印加電圧によりポテンシャル電位Φ(V)の位置変化は小さくなる。E0=-2E+5(V/m)は逆に順方向の印加電圧であり、ポテンシャル電位Φ(V)の位置変化は大きくなる。

  2. 　電界E(V/m)の電界初期値の影響

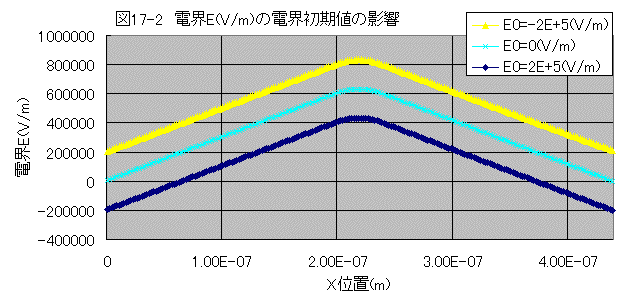
    　電界E(V/m)は電界初期値により、ほぼ平行にシフトする。

  3. 　正孔密度[po](個/m^3)の電界初期値の影響

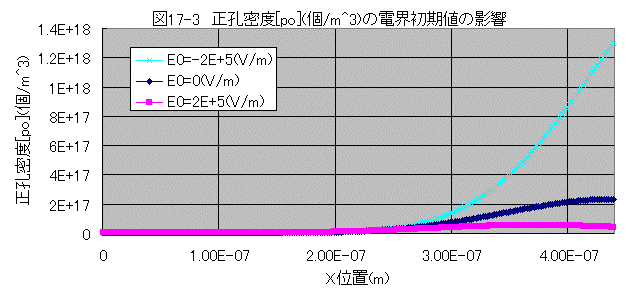
    　正孔密度[po]は順方向電圧印加で増大し、逆方向電圧印加で減少する。

  4. 　自由電子密度[no](個/m^3)の電界初期値の影響

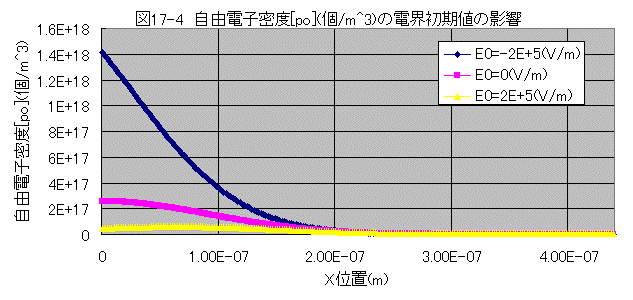
    　自由電子密度[po]は順方向電圧印加で増大し、逆方向電圧印加で減少する。

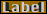  5. 　正味動きえる電荷(C/m^3)の電界初期値の影響

    　正味動きえる電荷(C/m^3)は順方向電圧印加で増大し、逆方向電圧印加で減少する。

  6. 　p-n接合の静電容量
    　正味動きえる電荷(C/m^3)は図17-5に示す様に印加電圧で変化する。全電荷容量は図17-5の中心から片側の積分で与えられる。
    　p-n接合の静電容量は印加電圧で変化し、可変容量として用いられることがある。この目的のダイオードをバリキャップダイオードと呼ぶ。これは主に自動周波数制御に用いられる。

  7. ダイオードのその他特性の纏め
    　以上の検討で明らかなように、「１６章：ダイオードの整流特性」で用いたモデルは相当大胆に単純化しており、正確なものではないことがわかる。
    　しかし、モデルを正確にするほど、計算量は膨大なものとなり実用上の問題が発生する。どこまで精密な計算を実施するかは、計算にかかる労力と計算結果から得られる効果のバランスで判断せざる得ないであろう。


  8. １８章：バイポーラ(BJT)トランジスタに行く。

  9. トップページに戻る。