光学系設計手法近軸理論（近軸理論の概要）
レンズの曲率と屈折率を考慮して光線追跡プログラムを使用して、レンズの曲率の最適化計算を行う際、 複雑な複合レンズにおいては、やみくもに計算しても解が求まらないことが多いです。
レンズの曲率の最適化計算で変数として与えることができるのは6変数程度が計算時間の関係で限度です。
複雑な複合レンズを設計するためには、最適化計算時間に無理が無い程度にレンズ群を分割し、各レンズ群 毎に設計パラメータ目標値を設定することが不可欠となります。
設計パラメータ目標値設定には近軸光線追跡による手法が有効です。
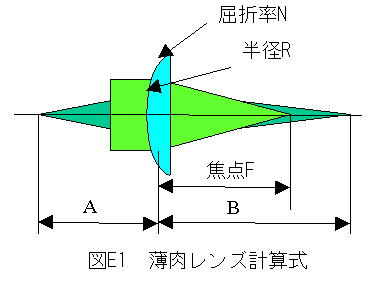
（１）薄肉レンズの式
図1に示す片凸レンズの半径Rと屈折率Nと
焦点距離Fの間には、下記の関係式が近似的に成立します。
F=R/(N-1) -----(E1)式
（２）薄肉レンズでの焦点距離と結像の関係式
図1に示す結像条件において、下記の関係式が成立します。
1/A + 1/B = 1/F -----(E2)式
(E2)式は単純な光学系には適用容易であるが複雑な光学系の 計算には適しません。
（３）レンズのパワー(φ)と焦点距離(F）の関係式
近軸光線追跡においては、焦点距離(F）を用いずにレンズのパワー(φ)を用いるのが一般的です。
Φ= 1/F -----(E3)式
レンズのパワー(φ)は焦点距離(F）を逆数にしたもので単位は(1/mm)である。
実際には、あまり大差はないのであるが、光線追跡では焦点距離「無限大」の条件入力が必要となるが、 「無限大」は入力できないので、1E10等の大きな数値で代用しなければなりません。
レンズのパワー(φ)は焦点距離(F） 「無限大」の時、零であるので計算しやすい特徴があります。
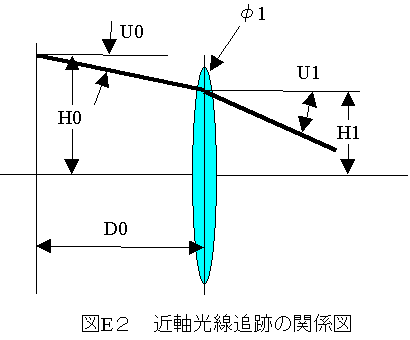
（４）近軸光線追跡の関係式
図E２の近軸光線追跡の関係図において、レンズφ1は 薄肉レンズであり、厚さはゼロです。
（実際は有り得えません。）
(a)入力パラメータ
D0：レンズ面までの距離(mm)
φ1：レンズのパワー(1/mm)
U0：入射光の角度(rad)
H0：入射光の高さ(mm)
(b)出力パラメータ
U1：出射光の角度(rad)
H1：出射光の高さ(mm)
(c)関係式
出力パラメータは下記関係式で計算します。（もともと近似式です。）
H1=H0 - D0*U0 -----(E4)式
U1=U0 + φ1*H1 -----(E5)式
(E4)式、 (E5)式で計算した出射光の角度と高さを入射光に置き換えることによって、次々と計算を進めることが できます。
(E4)式、 (E5)式は単純な計算であり、EXCELの表計算で十分に可能です。
近軸理論の計算は単純であり、あえて計算プログラムを作るほどではありませんので 説明はこの程度で終わらせていただきます。
３次元光線追跡の関係式
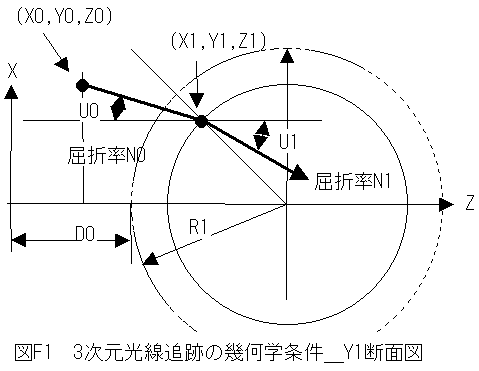
３次元光線追跡の説明図を正確に2次元の紙面に描くのは難しいです。図F1はX,Y,Zの3次元座標系においてY1の位置における断面図を示します。
（１）入力パラメータ
図の幾何学条件図において入力パラメータは下記のとおりです。
Z0：入射光光軸方向座標
X0：入射光像高X方向座標
U0：入射光のX方向角度
Y0：入射光像高Y方向座標
V0：入射光のY方向角度
R1：レンズ面の曲率半径
D0：レンズ面の光軸方向距離
Ox1：レンズX方向オフセット
Oy1：レンズy方向オフセット
N0：入射側の屈折率
N1：出射側の屈折率
（２）中間パラメータ
詳細は別途詳細図による。
（３）出力パラメータ
Z1：出射光光軸方向座標
X1：出射光像高X方向座標
U1：出射光のX方向角度
Y1：出射光像高Y方向座標
V1：出射光のY方向角度
（４）線と球面の関係式
入射光の直線の方程式から
X1=X0 - (tan(U0))*(Z1 - Z0) -------(F1)式
Y1=Y0 - (tan(V0))*(Z1 - Z0) -------(F2)式
レンズ面の球の方程式から
(X1-Ox1)2 +(Y1-Oy1)2 +(Z1- D0 -R1) 2 = R12 -------(F3)式
の関係式が成立します。
（F１）（F２）（F３）式より、光線とレンズ面の交点（X1,Y1,Z1)を求めることができます。
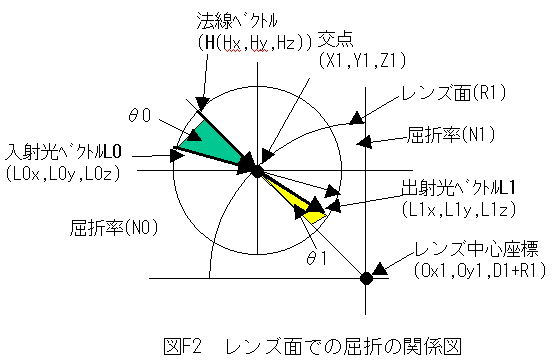
（５）レンズ面での屈折の関係式
3次元的なレンズ面での屈折の関係図を2次元の紙面に書くのは大変難しいです。図F2は、レンズの球の中心と入射光方向ベクトルを含む断面図で表している。従って、XYZ座標軸は任意の角度(3次元)で回転しているので注意が必要でです。
図F2において、法線ベクトルHは交点
(X1,Y1,Z1)における法線の単位ベクトルで す。ここで
Hx=(-X1+Ox1)/R1 ---(F4)式
Hy=(-Y1+Oy1)/R1 ---(F5)式
Hz=(-Z1+D1+R1)/R1 ---(F6)式
の関係が成立します。
また、ベクトルHの絶対値|H|は
|H|=SQRT(Hx2+Hy2+Hz2)=1---(F7)式
です。
同様に入射光もベクトルL0で定義されます。
ベクトルL0の絶対値|L0|は
|L0|=SQRT(L0x2+L0y2+L0z2)=1---(F8)式
の単位ベクトルとします。
ここで、X,Y,Z座標系での光線角度U0.V0とは下記の関係式が成立します。
L0x/L0z=-TAN(U0) -------(F9)式
L0y/L0z=-TAN(V0) -------(F10)式
L0z=SQRT(1-L0x2-L0y2) -----(F11)式
ところで、２つのベクトルHとL0の大きさとそのそのなす角の余弦との積は、ベクトルの内積またはスカラー積といいます。即ち
|H|*|L0|*COS(θ0)=H*L0
|H|= |L0|=1であり、ベクトルの内積の公式から、
COS(θ0)=Hx*L0x+Hy*L0y+Hz*L0z -----(F12)式
(F12)式の誘導にあたっては、説明図を用いずにベクトルの公式を使用しました。公式の証明は 数学の参考書を参照願います。
次に屈折の法則から、
N0*SIN(θ0)=N1* SIN(θ1) -----(F13)式
が成立します。
(F13)式から屈折角θ1を求めることができます。屈折角θ1から出射ベクトルL1を求めるため
図F3に示す関係を用います。
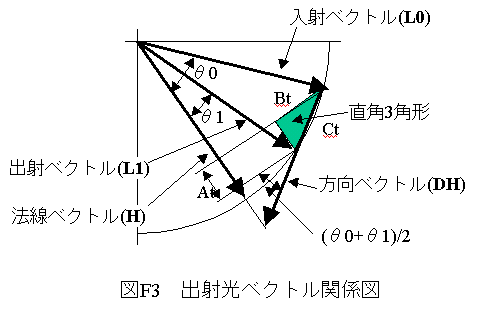
図F3において、入射ベクトルと出射ベクトルの差分 DLは直角3三角形abcで表わされます。
ここで、 θ0 > θ1の場合、
At=COS(θ1)- COS(θ0) -----(F14)式
Bt=SIN(θ0)-SIN(θ1) -----(F15)式
Ct=SQRT(At2+Bt2) -----(F16)式
差分ベクトルDLの方向ベクトルDHは近似的に
DH=H-L0 -----(F17)式
となりますが、正確には補正が必要です。
法線ベクトルの絶対値の補正係数Khは下記式となります。
Kh=COS(θ1)+SIN(θ1)*TAN((θ0+ θ1)/2) -----(F18)式
補正後の方向ベクトルDHは下記式となります。
DH=Kh*H-L0 -----(F19)式
逆にθ0 < θ1の場合、
At=COS(θ0)- COS(θ1) -----(F20)式
Bt=SIN(θ1)-SIN(θ0) -----(F21)式
Ct=SQRT(At2+Bt2) -----(F22)式
法線ベクトルの絶対値の補正係数Khは下記式となります。
Kh=COS(θ0)+SIN(θ0)*TAN((θ0+ θ1)/2) -----(F23)式
DH=-Kh*H+L0 -----(F19)式
従って、入射ベクトルと出射ベクトルの差分DLは下記式となります。
DL=Ct*DH/|DH| -----(F24)式 （ |DH| はDHの絶対値）
最終的に求める出射ベクトル(L1)は下記式となります。
L1=L0+DL -----(F25)式
ここで、X,Y,Z座標系での出射光線角度U1.V1とは下記の関係式が成立します。
TAN(U1)= -L1x/L1z -------(F26)式
TAN(V1)= -L1y/L1z -------(F27)式
(F12)式〜 (F25)式により、出射ベクトル(L1)を求めることができます。
上記式の一部は一般的になじみの薄いベクトルの式で表わしており、実際の計算は、XYZ成分に 分けて計算する必要があります。また、ベクトルは方向を持っており、数値の正負の方向に十分注意が 必要です。
3次元の光線追跡計算式は、かなり複雑です。
ミラー反射光学系
ミラー反射光学系の場合、反射の法則から、
θ0=θ1 -----(G13)式
が成立します。
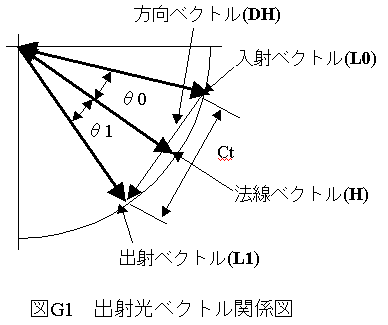
(G13)式から反射角θ1を求めることができます。反射角θ1から出射ベクトルL1を求めるため 図G1に示す関係を用います。
図G1において、入射ベクトルと出射ベクトルの差分DLは直角3三角形abcで表わされます。
Ct=2*SIN(θ0) -----(G16)式
差分ベクトルDLの方向ベクトルDHは近似的に
DH=H-L0 -----(G17)式
となりますが、正確には補正が必要です。
法線ベクトルの絶対値の補正係数Khは下記式となります。
Kh=COS(θ1) -----(G18)式
補正後の方向ベクトルDHは下記式となります。
DH=Kh*H-L0 -----(G19)式
従って、入射ベクトルと出射ベクトルの差分DLは下記式となります。
DL=Ct*DH/|DH| -----(G24)式 （ |DH| はDHの絶対値）
最終的に求める出射ベクトル(L1)は下記式となります。
L1=L0+DL -----(G25)式
ここで、X,Y,Z座標系での出射光線角度U1.V1とは下記の関係式が成立します。
TAN(U1)= -L1x/L1z -------(G26)式
TAN(V1)= -L1y/L1z -------(G27)式
最後にミラー反転処理が必要となります。
Z1’=2*D0-Z1-------(G27)式
X1’=X1-------(G28)式
Y1’=Y1-------(G29)式
U1’=-U1-------(G30)式
V1’=-V1-------(G31)式
ミラー反射の条件式以外は基本的に屈折光学系と同じとなります。
アクロマートレンズ設計事例に行く。ミラープロジェクション設計事例に行く。