オームの法則電流（I）は電圧（E）に比例し、抵抗(R)に反比例する。
電力（仕事率)(P)電力（仕事率)(P)は
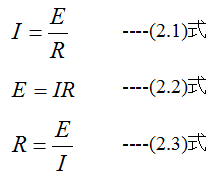
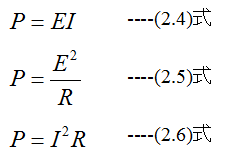
例題2-1 100V、40Wの電球の電流はいくらか？解答
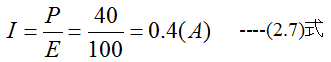
銅絶縁電線の許容電流（A)銅絶縁電線の許容電流（A)を表2-1に示します。
表2-1 銅絶縁電線の許容電流（A)
| 断面積（ｍｍ＾2） | 綿絶縁線 | ゴム絶縁線 |
| 0.79 | - | 16 |
| 1.13 | 19 | 19 |
| 2.01 | 27 | 27 |
| 3.14 | 35 | 35 |
| 5.31 | 48 | 48 |
| 8.04 | 63 | 63 |
| 12.6 | 83 | 81 |
| 14 | 91 | 88 |
| 22 | 122 | 115 |
| 30 | 145 | 139 |
| 38 | 170 | 162 |
| 50 | 201 | 190 |
| 80 | 276 | 257 |
| 100 | 322 | 298 |
| 200 | 490 | 469 |
コードの許容電流コードの許容電流を表2-2に示します。
表2-2 コードの許容電流
| 公称断面積(mm＾2) | 素線数/径(mm) | 許容電流(A) |
| 0.75 | 30/0.18 | 7 |
| 0.75 | 30/0.18 | 7 |
| 1.25 | 50/0.18 | 12 |
| 2 | 37/0.26 | 17 |
| 3.5 | 45/0.32 | 23 |
| 5.5 | 70/0.32 | 35 |
例題2-2表2-1 銅絶縁電線の許容電流（A)において、長さ10m当たりの許容電流での消費電力を計算せよ。ただし 、銅線の固有抵抗をρ＝1.724E-8（Ωm）とする。
解答 計算結果を以下に示します。
| 断面積（ｍｍ＾2） | ゴム絶縁線電流（A) | 抵抗値（Ω/10m) | 消費電力（W) |
| 0.79 | 16 | 0.22 | 56.2 |
| 0.79 | 16 | 0.22 | 55 |
| 1.13 | 19 | 0.152 | 62.5 |
| 2.01 | 27 | 0.0857 | 67.2 |
| 3.14 | 35 | 0.0549 | 74.8 |
| 5.31 | 48 | 0.0325 | 85.1 |
| 12.6 | 81 | 0.0137 | 90 |
| 14 | 88 | 0.0123 | 95.4 |
| 22 | 115 | 0.00784 | 103.6 |
| 30 | 139 | 0.00575 | 111 |
| 38 | 162 | 0.00454 | 119.1 |
| 50 | 190 | 0.00345 | 124.5 |
| 80 | 257 | 0.00216 | 142.3 |
| 100 | 298 | 0.00172 | 153.1 |
| 200 | 469 | 0.00086 | 189.6 |
「2-1.xls 」にいく。 例題2-3表2-2 コードの許容電流（A)において、長さ10m当たりの許容電流での消費電力を計算せよ。ただし、銅線の 固有抵抗をρ＝1.724E-8（Ωm）とする。
解答 計算結果を以下に示します。
| 断面積（ｍｍ＾2） | コードの許容電流（A) | 抵抗値（Ω/10m) | 消費電力（W) |
| 0.75 | 7 | 0.23 | 11.3 |
| 1.25 | 12 | 0.138 | 19.9 |
| 2 | 17 | 0.0862 | 24.9 |
| 3.5 | 23 | 0.0493 | 26.1 |
| 5.5 | 35 | 0.0313 | 38.4 |
「2-2.xls 」にいく。 抵抗の直列結合ｎ個の抵抗Ri(i=1,2,…,n）を直列結合した場合の合成抵抗Rは
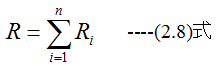
となります。
抵抗の並列結合ｎ個の抵抗Ri(i=1,2,…,n）を並列結合した場合の合成抵抗Rは
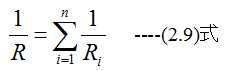
となります。
例題2-4起電力24Vの電池に5.5Ωの抵抗をつないだら4Aの電流が流れた。この電池の内部抵抗はいくらか？
解答
5.5Ωの抵抗をR1、内部抵抗をR2とするならば
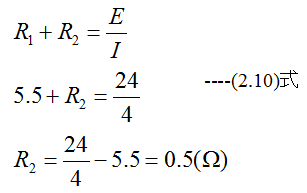
となります。