１７章：片持ち梁の計算

作成2012.11.03

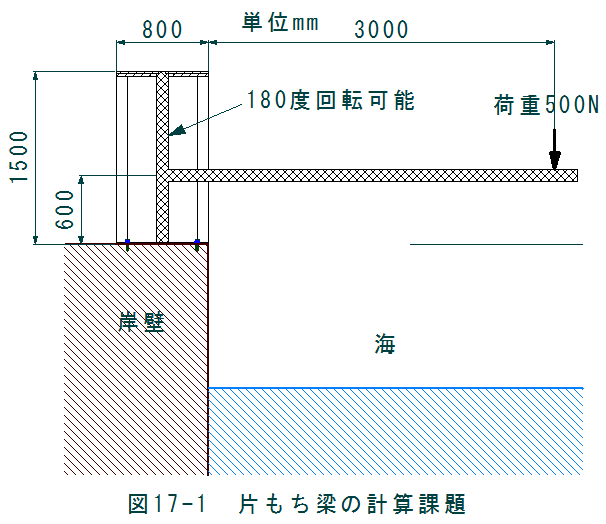
　図17-1に示すように岸壁から3000mm離れた位置に測定機をとりつけたい。
　測定機は180度回転して、取付調整をおこないたい。この場合、どのような構造ににべきか？

　この課題に対する解答は無限にありますが、よく検討しないと強度不足となったり、自重が大きくなって、運搬・組立が難しくなったりします。

H鋼の梁を使用
　H鋼は強度計算に必要な定数が機械工学便覧に記載されており、最も強度計算が容易な例です。欠点はH鋼はmあたりの質量が大きく重いため、運搬と設置工事が大変です。

　強度計算結果を以下に示します。

100×50H鋼強度計算表（片もち支持）
項目	記号（＝計算式）	値	単位
ヤング率	E	205800	N/mm^2
断面2次モーメント	I	1870000	mm^4
断面係数	Z	37500	mm＾3
梁の長さ	L	3400	mm
集中荷重	W	500	N
等分布荷重	w	0.09114	N/mm
梁の重量	G=ｗL	309.876	N
集中荷重の計算
項目	記号（＝計算式）	値	単位
最大モーメント	M1=WL	1700000	Nmm
最大応力	σ1＝M1/Z	45.3333333333333	N/mm^2
最大歪	δ1=WL^3/(3EI)	17.0215272256089	mm
等分布荷重の計算
項目	記号（＝計算式）	値	単位
最大モーメント	M2=wL^2/2	526789.2	Nmm
最大応力	σ2＝M2/Z	14.047712	N/mm^2
最大歪	δ2=wl^3/(8EI)	0.00116350649350649	mm
集中荷重+等分布荷重の計算
項目	記号（＝計算式）	値	単位
最大モーメント	M=M1+M2	2226789.2	Nmm
最大応力	σ＝σ1+σ2	59.3810453333333	N/mm^2
最大歪	δ=δ1+δ2	17.0226907321024	mm

EXCEL計算シートは以下で参照できます。

「100×50H鋼強度計算表（片もち支持）」にいく。

　SS400材の耐力は215（N/mm^2）であり強度的には問題が無いことがわかります。最大撓みが17.0mmもありますがこれも問題ないでしょう。
　強度計算が容易で、加工も素材を一定の長さに切るだけですので容易でしょう。しかし梁の重量は310N（31.6ｋｇ）もありますので、運搬と設置工事は重量物の扱いが必要となります。

トラス構造
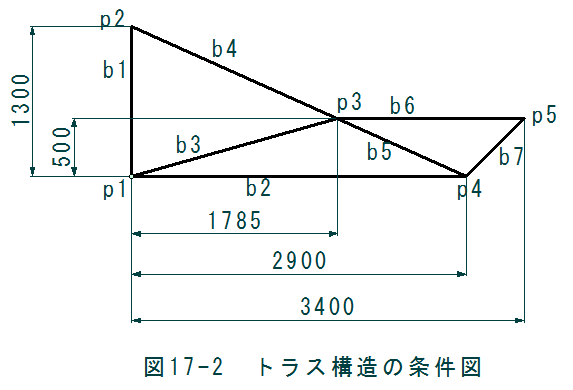
　図17-2にトラス構造の条件図を示します。節点は5個、部材番号は7であり、結構複雑な条件となります。

基本計算条件

項目	記号	値	単位	備考
節点数	Jn	5	点	最大100点
要素数	En	7	本	最大100本
外力の加わる節点数	Ns	1	点	最大100点
節点2の固定条件	Fixn	1	モード選択	0or1or2

節点座標

節点番号	X座標(mm)	Y座標(mm)	支持条件
1	0	0	XY固定
2	0	1300	モード選択
3	1785	500
4	2900	0
5	3400	500

荷重条件

節点番号	荷重Wx（N)	荷重Wｙ（N)
5	0	-500

部材条件

部材番号	節点Pi	節点Pｊ	ヤング率E(N/mm2)	断面積A（ｍｍ2）
1	1	2	205800	50
2	1	4	205800	50
3	1	3	205800	50
4	2	3	205800	50
5	3	4	205800	50
6	3	5	205800	50
7	4	5	205800	50

変位計算結果

節点番号	変位Δｘ(mm)	変位Δｙ(mm)
1	0	0
2	0	-0.0740432227312694
3	0.164318641788556	-0.373473988077913
4	-0.455150631681244	-2.1095425382884
5	0.24279288863015	-2.87620391877342

応力・軸力計算結果

部材番号	応力σ(N/mm2)	軸力F（N)	部材長さ（ｍｍ）	質量（ｋｇ）
1	-11.7216117216117	-586.080586080586	1300	0.51025
2	-32.3	-1615	2900	1.13825
3	6.38272308819541	319.13615440977	1853.70574795462	0.727579506072189
4	28.6604230602285	1433.02115301143	1956.0738738606	0.767758995490284
5	24.4395171801736	1221.97585900868	1221.97585900868	0.479625524660907
6	10	500	1615	0.6338875
7	-14.142135623731	-707.10678118655	707.106781186548	0.27753941161572

　H鋼では部材質量が31.6kg、変位量が17mmに対して、トラス構造では質量は5.4kg、変位量は2.9mmと小さくなります。ただし、部材1、2、7は圧縮荷重を受けるので坐屈強度の配慮が必要となります。

トラス計算プログラム
　部材長さの出力を追加しました。（重量計算容易化のため）
　下記のトラスの計算3.xls(フリーソフト)]をダウンロードしてください。

　ダウンロード後は解凍してから使用してください。
トラスの計算3.xls(フリーソフト)]をダウンロードする。

坐屈荷重の計算
　部材2がもっとも坐屈しやすいため、ＳＧＰ（配管用炭素鋼鋼管）25A（外形Φ34、内径Φ27.6）を使用し、部材1と部材7は20A（外形Φ27.2、内径Φ21.6）として坐屈強度計算をおこなった結果を下記に示します。

項目	記号（＝計算式）	部材1	部材2	部材7	単位
ヤング率	E	205800	205800	205800	N/mm^2
外形	ｄ1	27.2	34	27.2	mm
内径	ｄ2	21.6	27.6	21.6	mm
長さ	L	1300	2900	707	mm
断面2次モーメント	I=π（d1^4-d2^4)/64	16183.3742010314	37112.8956804659	16183.3742010314	mm^4
断面係数	Z=π(d1^3-d2^3)/32	986.259031297365	1794.5782546954	986.259031297365	mm＾3
断面積	A=π(d1^2-d2^2)/4	214.633610093255	309.63537193781	214.633610093255	mm＾4
最小断面2次半径	K=SQRT(I/A)	8.68331733843696	10.948059188733	8.68331733843696	mm
長柱の細長さ比	λ=L/k	149.712367904086	264.887132048436	81.4204954678373	無次元
両端回転の場合	n	1	1	1
坐屈応力（オイラーの理論公式）	σcr＝ｎ（π＾2）E/λ＾2	90.6211892101254	28.9483219081211	306.392149959512	N/mm^2
軸力	F	586	1615	707	N
圧縮応力	σ＝F/A	2.73023409402373	5.21581235985006	3.29398550251669	N/mm^2
安全率	S=σcr/σ	33.1917286537766	5.55010800061705	93.0156340170351	判定OK
比重	ρ	0.00000785	0.00000785	0.00000785	ｋｇ/ｍｍ＾3
部材質量	G＝ρAL	2.19033599100166	7.04884924216424	1.19120580433706	kg

EXCEL計算シートは以下で参照できます。

「坐屈強度計算表」にいく。

　部材2の質量が最大でしつ量7kgとなります。トラスの再計算を行うと
変位計算結果

節点番号	変位Δｘ(mm)	変位Δｙ(mm)
1	0	0
2	0	-0.0172193541235509
3	0.154523534077679	-0.338505453550084
4	-0.0734113922066517	-1.20145240953697
5	0.232997780919273	-1.52384248037769

応力・軸力計算結果

部材番号	応力σ(N/mm2)	軸力F（N)	部材長さ（ｍｍ）	質量（ｋｇ）
1	-2.72595621432829	-586.080586080582	1300	2.194075
2	-5.2096774193548	-1614.99999999999	2900	7.05715
3	6.38272308819536	319.136154409768	1853.70574795462	0.727579506072189
4	28.6604230602283	1433.02115301142	1956.0738738606	0.767758995490284
5	24.4395171801734	1221.97585900867	1221.97585900868	0.479625524660907
6	9.99999999999994	499.999999999997	1615	0.6338875
7	-3.28886874970489	-707.106781186552	707.106781186548	1.1934194699476

　となり、最大変位が1.5mm、総質量が13kgとなります。実際には回転部分の質量増加があり、回転部分の総質量は約15kg程度となることが予想できます。

回転軸の強度計算
　回転軸も一応強度計算が必要です。計算結果を下記に示します。

回転軸強度計算結果

項目	記号（＝計算式）	値	単位
片もち梁の全長	L	3400	ｍｍ
集中荷重	W	500	N
片もち梁の全質量	Gm	15	kg
片もち梁のｊ重心位置	Gｘ	1500	mm
最大モーメント	M＝LW+ｇGmGx	1920500	Nmm
回転軸のスパン	Ls	1460	mm
ラジアル荷重	Wr＝M/Ls	1315.41095890411	N
軸受け直径	ｄ	20	mm
せん断応力	τ＝4Wr/(πｄ＾2）	4.18708312613678	N/mm2
許容せん断応力	τmax	80	N/mm2
安全率	S=τmax/τ	19.1063796896271

　上記表において、重心位置と許容せん断応力は大まかな値を設定していますが、安全率を19と大きくしてあるため、厳密な値である必要はありません。回転軸の直径は約Φ20mmで十分ということになります。

EXCEL計算シートは以下で参照できます。

「回転軸強度計算表」にいく。

架台の強度計算
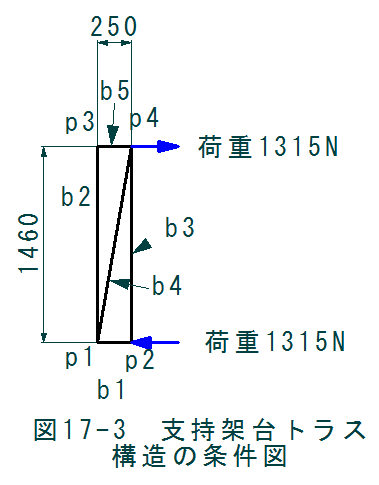
支持架台の計算条件を図17-3に示します。

基本計算条件

項目	記号	値	単位	備考
節点数	Jn	4	点	最大100点
要素数	En	5	本	最大100本
外力の加わる節点数	Ns	2	点	最大100点
節点2の固定条件	Fixn	2	モード選択	0or1or2

節点座標

節点番号	X座標(mm)	Y座標(mm)	支持条件
1	0	0	XY固定
2	250	0	モード選択
3	0	1460
4	250	1460

荷重条件

節点番号	荷重Wx（N)	荷重Wｙ（N)
2	-1315	0
4	1315	0

部材条件

部材番号	節点Pi	節点Pｊ	ヤング率E(N/mm2)	断面積A（ｍｍ2）
1	1	2	205800	250
2	1	3	205800	250
3	2	4	205800	250
4	1	4	205800	250
5	3	4	205800	250

変位計算結果

節点番号	変位Δｘ(mm)	変位Δｙ(mm)
1	0	0
2	-0.00638969873663751	0
3	2.6017403428953	0

応力・軸力計算結果

部材番号	応力σ(N/mm2)	軸力F（N)	部材長さ（ｍｍ）	質量（ｋｇ）
1	-5.26	-1315	250	0.490625
2	0	0	1460	2.86525
3	-30.7183999999993	-7679.59999999984	1460	2.86525
4	31.165488902951	7791.37222573774	1481.24947257375	2.90695208992598
5	0	0	250	0.490625

　架線トラスの変位は2.6mm、総質量は約10kgになることがわかります。部材1と部材3は圧縮荷重を受けるため、坐屈強度の計算が必要となります。

坐屈荷重の計算
　部材3がもっとも坐屈しやすいため、ＳＧＰ（配管用炭素鋼鋼管）25A（外形Φ34、内径Φ27.6）を使用し、部材1は20A（外形Φ27.2、内径Φ21.6）として坐屈強度計算をおこなった結果を下記に示します。

項目	記号（＝計算式）	部材1	部材3	単位
ヤング率	E	205800	205800	N/mm^2
外形	ｄ1	27.2	34	mm
内径	ｄ2	21.6	27.6	mm
長さ	L	250	1460	mm
断面2次モーメント	I=π（d1^4-d2^4)/64	16183.3742010314	37112.8956804659	mm^4
断面係数	Z=π(d1^3-d2^3)/32	986.259031297365	1794.5782546954	mm＾3
断面積	A=π(d1^2-d2^2)/4	214.633610093255	309.63537193781	mm＾4
最小断面2次半径	K=SQRT(I/A)	8.68331733843696	10.948059188733	mm
長柱の細長さ比	λ=L/k	28.7908399815549	133.356969927833	無次元
両端回転の場合	n	1	1
坐屈応力（オイラーの理論公式）	σcr＝ｎ（π＾2）E/λ＾2	2450.39695624179	114.212510436901	N/mm^2
軸力	F	1315	7680	N
圧縮応力	σ＝F/A	6.12671985263005	24.8033677545811	N/mm^2
安全率	S=σcr/σ	399.952505611938	4.60471785795324	判定OK
比重	ρ	0.00000785	0.00000785	ｋｇ/ｍｍ＾3
部材質量	G＝ρAL	0.421218459808012	3.54873099777924	kg

　部材1や部材5はアンカー固定、回転軸固定のため、より複雑な形状となり、架台の質量も大きくなります。ただし、架台は地上に設置されるため、重量物の運搬・設置は容易となります。
EXCEL計算シートは以下で参照できます。

「坐屈強度計算表」にいく。

ケミカルアンカー強度
　ケミカルアンカー強度の計算表を下記に示します。
15:16 2012/11/03
ケミカルアンカー強度計算表

No	項目	記号	値	単位	備考
1	全ネジボルト安全率	S1	2	無次元	要設定
2	接着系アンカーのせん断安全率	S2	0	無次元	自動計算
3	コンクリートのコーン状破壊安全率	S3	0	無次元	自動計算
4	全ネジボルトの耐力	σｙ	205	N/mm2	要設定
5	既存コンクリートの設計基準強度	σb	21	N/mm2	標準値
6	接着系アンカーのせん断強度	τa	10	N/mm2	自動計算

No	名称	外径	谷径	穿孔深さ	有効穿孔深さ	水平投影面積	全ネジボルト許容張力	せん断の許容引張力	コーン状破壊の許容引張力	総合許容張力
		ｄ（ｍｍ）	ｄ1（ｍｍ）	L(mm)	Le(mm)	A(mm2)	F1（N)	F2（N)	F3（N)	F（N)
1	M12-80	12	10.106	80	68	17203	8222	7675	5429	5429
2	M12-100	12	10.106	100	88	27759	8222	9933	8760	8222
3	M12-120	12	10.106	120	108	40828	8222	12190	12884	8222
4	M12-140	12	10.106	140	128	56410	8222	14448	17801	8222
5	M16-100	16	13.835	100	84	26590	15409	12642	8391	8391
6	M16-120	16	13.835	120	104	39408	15409	15652	12436	12436
7	M16-140	16	13.835	140	124	54739	15409	18661	17274	15409
8	M16-160	16	13.835	160	144	72583	15409	21671	22905	15409
9	M20-120	20	17.294	120	100	38013	24077	18812	11996	11996
10	M20-140	20	17.294	140	120	53093	24077	22574	16754	16754
11	M20-160	20	17.294	160	140	70686	24077	26337	22306	22306
12	M20-180	20	17.294	180	160	90792	24077	30099	28651	24077
13	M20-200	20	17.294	200	180	113411	24077	33861	35789	24077

　上記表からM20で穿孔深さ180mmのケミカルアンカーの強度は安全率2で1本あたり24077Nとなります。この場合の安全率の計算は以下のようになります。

No	項目	記号（＝計算式）	値	単位
1	片もち梁の全長	L	3400	ｍｍ
2	集中荷重	W	500	N
3	片もち梁の全質量	Gm	15	kg
4	片もち梁のｊ重心位置	Gｘ	1500	mm
5	最大モーメント	M＝LW+ｇGmGx	1920500	Nmm
6	アンカーのスパン	La	700	mm
7	片側アンカー本数	Na	2	本
8	アンカー張力	Wa=M/(LaNa)	1371.7857	N/本
9	アンカー許容張力	Fn	24077	N/本
10	安全率	S=Fn/Wa	17.551575

EXCEL計算シートは以下で参照できます。

「アンカー強度計算表」にいく。

　アンカー許容張力にも安全率2がかかっていますので、強度は十分であることがわかります。これで、大まかですが十分な強度を持つ構造設計が可能であることがわかります。
　具体的な構造設計では、種々の理由で部材の詳細形状が変更になりますが、安全サイドに変更する場合は問題ありません。

１８章：線形計画法（シンプレックス法）に行く。

トップページに戻る。